주어진 수열 $(a_n)$이 임의의 양의 정수 $n \in \mathbb{N}$에 대하여, $a_n = n \cdot a_{n-1}$이라는 관계를 만족한다고 가정하자. 이 수열의 초항 $a_1 = 1$이라 하면, \begin{align*} a_n & = n \cdot a_{n-1} \\[1ex] & = n \cdot (n-1) \cdot a_{n-2} \\[1ex] & = n \cdot (n-1) \cdot (n-2) \cdot a_{n-3} \\ & \;\;\vdots \\ & = n \cdot (n-1) \cdot (n-2) \cdots 3 \cdot 2 \cdot a_{1} \end{align*} 이 되어 $a_n = n!$을 얻는다. 따라서 주어진 수열 $(a_n)$은 $n$에 대한 계승(factorial)을 나타냄을 알 수 있다.
$ $
위와 같은 방법으로 일반적으로 수열 $(a_n)$의 처음 몇 개의 항이 주어지고, $a_n$을 $a_1,\, \ldots,\, a_{n-1}$의 값에 대한 함수로써 나타낼 수 있다면, 모든 양의 정수 $n \in \mathbb{N}$에 대하여 $a_n$의 값을 구할 수 있다.
$ $
$ $
예제 2.1.2.
Q. 평면 위에 서로 교차하는 $n$개의 직선으로 나뉘는 영역의 최대 개수를 $a_n$이라 할 때 수열 $(a_n)$에 대한 점화식을 구하여라. (단, 어느 세 직선도 동시에 한 점에서 만나지 않는다.)
A. 다음 그림을 통해
$ $

$ $
$a_1 = 2$, $a_2 = 4$, $a_3 = 7$임을 알 수 있다. 평면에 $(n-1)$개의 직선으로 $a_{n-1}$개의 영역이 생겼다고 하자. 이제 여기에 $n$번째 직선을 하나 더 그리면 그 직선이 다른 $(n-1)$개의 직선과 만날 때마다 새로운 영역이 하나 더 생기고 마지막 만나는 직선을 지나서는 하나의 영역이 더 생기므로 총 $n$개의 새로운 영역이 생긴다. 따라서 \[ a_n = a_{n-1} + n \quad (n \geq 2) \] 또한 초기조건 $a_1 = 2$이다. $ $
$ $
예제 2.1.3.
Q. 평면 위에 서로 다른 두 점에서 교차하는 $n$개의 원으로 나뉘는 영역의 최대 개수를 $a_n$이라 할 때 수열 $(a_n)$에 대한 점화식을 구하여라. (단, 어느 세 원도 동시에 한 점에서 만나지 않는다.)
A. 다음 그림을 통해
$ $

$ $
$a_1 = 2$, $a_2 = 4$, $a_3 = 8$임을 알 수 있다. 평면에 $(n-1)$개의 원으로 $a_{n-1}$개의 영역이 생겼다고 하자. 이제 여기에 $n$번째 원을 하나 더 그리면리그 원이 다른 $(n-1)$개의 원과 두 점에서 만날 때마다 두개의 영역이 새로 생기므로 총 $2(n-1)$개의 새로운 영역이 생긴다. 따라서 \[ a_n = a_{n-1} + 2(n-2) \quad (n \geq 2) \] 또한 초기조건 $a_1 = 2$이다. $ $
$ $
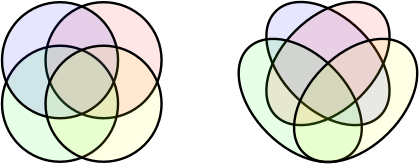
참고. 위 예제 2.1.3.에서 $a_4 = 14$이므로 원 $4$개로 이루어진 벤 다이어그램(Venn diagram)은 존재하지 않는다는 사실을 알 수 있다.
$ $
$ $
위 그림에서 왼쪽의 다이어그램에서는 빨간색과 초록색 원들의 교집합과 노란색과 파란색 원들의 교집합이 포함되어 있지 않다. 오른쪽이 네 개의 타원을 이용하여 네 집합에 대한 벤 다이어그램을 그린 예이다. $ $
$ $
예제 2.1.4.
Q. 계단을 오르는데 한 번에 한 계단씩이나 두 계단 씩 오른다고 할 때, 이러한 방법으로 $n$개의 계단을 오를 수 있는 서로 다른 방법의 수를 $a_n$이라 하자. 수열 $(a_n)$에 대한 점화식과 초기조건을 구하여라.
A. 한 번에 한 계단 또는 두 계단을 오를 수 있으므로, $n$개의 계단을 오르는 방법의 수는 처음 한 계단을 오른 뒤 남은 $(n-1)$개의 계단을 오르는 방법의 수와 처음 두 계단을 오른 뒤 남은 $(n-2)$개의 계단을 오르는 방법의 수의 합과 같다. 따라서
\[ a_n = a_{n-1} + a_{n-2} \quad (n \geq 3) \]
또한 초기조건 $a_1 = 1$, $a_2 = 2$이다. $ $
$ $
예제 2.1.5.
Q. 카탈란 수(Catalan number) $C_n$은 $(n+1)$개의 항에 이항연산을 적용하는 순서의 경우의 수로 정의될 수 있음을 살펴보았었다. 이 사실을 이용하여 $C_n$에 대한 점화식과 초기조건을 구하여라.
A. 우선 $C_1 = 1$, $C_2 = 2$임은 쉽게 확인할 수 있다. 이제 $n+1$개의 항 $x_0,\, x_2,\, \ldots,\, x_n$에 포함되어 있는 $n$번의 이항연산 중 마지막으로 수행되는 이항연산을 생각해 보자. 마지막 이항연산을 기준으로 $k$개의 항의 곱으로 이루어진 앞부분과 나머지 $(n-k+1)$개의 항의 곱으로 이루어진 뒷부분으로 나눌 수 있다. 이 경우 앞부분의 항을 구성하는 경우의 수는 $C_{k-1}$이고 뒷부분의 항을 구성하는 경우의 수는 $C_{n-k}$가 된다. 이제 $k$가 취할 수 있는 값은 $k = 1,\, 2,\, \ldots,\, n$이므로
\[ C_n = C_0 C_{n-1} + C_1 C_{n-2} + \cdots + C_{n-1}C_0 \quad (n \geq 2) \]
또한 초기조건 $C_1 = 2$이다. $ $
$ $
점화식은 다음과 같이 크게 세 유형으로 나누어볼 수 있다.
- $a_n$을 $a_1,\, \ldots,\, a_{n-1}$의 선형결합으로 나타낸 형태의 점화식을 동차선형점화식(homogeneous linear recurrence relation)이라 한다. 따라서 적당한 상수 $c_1,\, \ldots,\, c_{n-1}$에 대하여 \[ a_n = c_1a_{n-1} + c_2a_{n-2} + \cdots c_{n-2}a_2 + c_{n-1}a_1 \] 로 나타낼 수 있다.
- 동차선형점화식에 $n$에 대한 함수 $f(n)$이 첨가된 형태의 점화식을 비동차선형점화식(nonhomogeneous linear recurrence relation)이라 한다. 즉, \[ a_n = c_1a_{n-1} + c_2a_{n-2} + \cdots c_{n-2}a_2 + c_{n-1}a_1 + f(n) \] 으로 나타낼 수 있다.
- 선형점화식이 아닌 모든 형태의 점화식을 비선형점화식(nonlinear recurrence relation)이라 한다. 예를 들어 \begin{align*} a_n & = na_{n-1}, \\[1ex] a_n & = a_{n_1}a_{1} + a_{n-2}a_{2} + \cdots + a_{1}a_{n-1}, \\[1ex] a_n & = r a_{n-1}(1 - a_{n-1}) \quad (r \in \mathbb{R}) \end{align*} 몇 가지 간단한 형태의 비선형점화식을 제외하면, 일반적인 비선형점화식의 일반항을 구하는 것은 거의 불가능하다.
$ $
특성다항식(characteristic polynomial)은 초기조건이 주어진 점화식의 일반항을 구하는데 유용하게 사용된다. 먼저 동차선형점화식의 일반항을 구하는 방법에 대해 살펴보자.
$ $
$ $
예를 들어 점화식 $a_n = 2a_{n-1} + a_{n_2} - 2a_{n-3}$에 대한 특성방정식은 \[ C(t) = t^3 - 2t^2 - t + 2 \] 으로 주어진다.
$ $
$ $
증명. 두 수열 $(x_n)$, $(y_n)$이 점화식 $\myblue{(2.1)}$을 만족한다고 가정하자. 그러면 \begin{align*} x_n = c_1 x_{n-1} + c_2 x_{n-2} + \cdots c_k x_{n-k} \\[1ex] y_n = c_1 y_{n-1} + c_2 y_{n-2} + \cdots c_k y_{n-k} \end{align*} 이 성립한다. 따라서 임의의 실수 $\alpha,\, \beta \in \mathbb{R}$에 대하여 \begin{align*} \alpha x_n + \beta y_n & = \alpha \big( c_1 x_{n-1} + c_2 x_{n-2} + \cdots c_k x_{n-k} \big) \\[1ex] & \qquad + \beta \big( c_1 y_{n-1} + c_2 y_{n-2} + \cdots c_k y_{n-k} \big) \\[1ex] & = c_1 \big( \alpha x_{n-1} + \beta y_{n-1} \big) + c_2 \big( \alpha x_{n-2} + \beta y_{n-2} \big) \\[1ex] & \qquad + \cdots + c_k \big( \alpha x_{n-k} + \beta y_{n-k} \big) \end{align*} 이므로 수열 $(\alpha x_n + \beta y_n)$ 또한 점화식 $\myblue{(2.1)}$을 만족한다. $ $
$ $
먼저 어떤 수열 $(a_n)$의 동차선형점화식에 대한 특성다항식이 서로 다른 근을 가지는 경우, $(a_n)$의 일반항을 구하는 방법에 대하여 살펴보자.
$ $
$ $
증명.
- 실수 $r$이 특성다항식 $\myblue{(2.2)}$의 한 근이라 하자. 그러면 \[ r^{k} - c_1 r^{k-1} - c_2 r^{k-2} - \cdots - c_{k-1} r - c_k = 0 \] 을 만족한다. 이제 위 식의 양변에 $r^{n-k}$를 곱하고 식을 정리하면 \[ r^{n} = c_1 r^{n-1} + c_2 r^{n-2} + \cdots + c_k r^{n-k} \] 을 얻는다. 따라서 수열 $(r^n)$은 점화식 $\myblue{(2.1)}$을 만족한다.
- 특성다항식 $\myblue{(2.2)}$가 $k$개의 서로 다른 근 $r_1,\, \ldots,\, r_k$를 갖는다고 가정하자. 그러면 정리 2.1.7 $\myblue{\text{(a)}}$에 의해 다음 $k$개의 수열
\[ (r_1^n),\, (r_2^n),\, \ldots,\, (r_k^n) \]
은 모두 점화식 $\myblue{(2.1)}$을 만족한다. 따라서 정리 2.1.7 $\myblue{\text{(b)}}$에 의해 수열
\[ b_n = \alpha_1 r_1^n + \alpha_2 r_2^n + \cdots \alpha_k r_k^n \]
또한 점화식 $\myblue{(2.1)}$을 만족한다.
이제 점화식 $\myblue{(2.1)}$에 대한 초기조건 $a_0,\, \ldots,\, a_{k-1}$이 주어졌다고 하고 $\alpha_1,\, \ldots,\, \alpha_k$에 관한 선형연립방정식 \begin{align*} \alpha_1 r_1^0 + \alpha_2 r_2^0 + \cdots \alpha_k r_k^0 & = a_0, \\[1ex] \alpha_1 r_1^1 + \alpha_2 r_2^1 + \cdots \alpha_k r_k^1 & = a_1, \\ & \;\;\vdots \\ \alpha_1 r_1^{k-1} + \alpha_2 r_2^{k-1} + \cdots \alpha_k r_k^{k-1} & = a_{k-1} \end{align*} 을 생각해 보자. 위 선형연립방정식의 $k \times k$ 계수행렬 \[ A = \left[ \begin{matrix} 1 & 1 & \cdots & 1 \\ r_1 & r_2 & \cdots & r_k \\ \vdots & \vdots & \ddots & \vdots \\ r_1^{k-1} & r_2^{k-1} & \cdots & r_k^{k-1} \end{matrix} \right] \] 은 방데르몽드 행렬(Vendermonde matrix)이므로 $A$의 행렬식은 \[ \det(A) = \prod_{1 \leq i < j \leq k} (r_i - r_j) \neq 0 \] 으로 주어진다. 즉 계수행렬 $A$의 역행렬이 존재하므로 연립방정식은 유일한 해 $(\alpha_1^{\ast},\, \ldots,\, \alpha_{k-1}^{\ast})$를 갖는다. 그러면 수열 $(b_n)$은 점화식 $\myblue{(2.1)}$ 만족하면서 동시에 초기조건 또한 만족하므로, \[ a_n = b_n = \alpha_1^{\ast} r_1^n + \alpha_2^{\ast} r_2^n + \cdots \alpha_k^{\ast} r_k^n \] 이 수열 $(a_n)$의 일반항이 됨을 알 수 있다.
$ $
예제 2.1.9.
Q. 수열 $(a_n)$에 대한 점화식
\[ a_n = r a_{n-1} \]
과 초기값 $a_1 = a$가 주어졌을 때, 수열 $(a_n)$의 일반항을 구하여라.
A. 주어진 점화식에 대한 특성다항식은 $t - r = 0$이므로 해 $t = r$이다. 따라서 수열 $(\alpha r^n)$은 위 문제의 점화식을 만족한다. 이제 (선형연립)방정식 $\alpha r^{1} = \alpha r = a$를 만족하는 $\alpha$는 $\alpha = \dfrac{a}{r}$이다. 따라서 수열 $(a_n)$의 일반항은
\[ a_n = \frac{a}{r} r^n = a r^{n-1}. \tag*{$\myblue{\blacksquare}$} \]
$ $
예제 2.1.10.
Q. 수열 $(a_n)$에 대한 점화식
\[ a_n = 2a_{n-1} + a_{n-2} - 2a_{n-3} \]
과 초기값 $a_0 = 1$, $a_1 = 3$, $a_2 = -5$가 주어졌을 때, 수열 $(a_n)$의 일반항을 구하여라.
A. 주어진 점화식에 대한 특성다항식은
\[ t^3 - 2t^2 - t + 2 = 0 \]
으로 주어지며 위 다항식은 서로 다른 세 근 $t = 1,\, -1,\, 2$를 갖는다. 따라서
다음 수열
\[ \big( \alpha_1 + \alpha_2 (-1)^n + \alpha_3 2^n \big) \]
은 주어진 점화식을 만족한다. 이제 주어진 초기조건 $a_0 = 1$, $a_1 = 3$, $a_2 = -5$을 이용하여 선형연립방정식
\[ \systeme[\alpha_1\alpha_2\alpha_3]{\alpha_1 + \alpha_2 + \alpha_3 = 1,
\alpha_1 - \alpha_2 + 2\alpha_3 = 3,
\alpha_1 + \alpha_2 + 4 \alpha_3 = -5} \]
을 만족하는 해를 찾아야 한다. 위 선형연립방정식을 풀면 $\alpha_1 = 5$, $\alpha_2 = -2$, $\alpha_3 = -2$이므로 수열 $(a_n)$의 일반항은
\[ a_n = 5 - 2(-1)^n - 2^{n+1}. \tag*{$\myblue{\blacksquare}$} \]
$ $
수열 $(a_n)$의 동차선형점화식에 대한 특성다항식이 중근을 가지는 경우에는 $(a_n)$의 일반항을 다음과 같은 방법으로 구할 수 있다.
$ $
$ $
증명.
- $r$이 특성방정식 $\myblue{(2.2)}$의 한 근이므로 정리 2.1.8 $\myblue{\text{(a)}}$에 의해 수열 $(r^n)$은 점화식 $\myblue{(2.1)}$을 만족한다. 이제 $D(t) = t^{n-k}C(t)$로 정의하자. 그러면
\[ D(t) = t^n - c_1t^{n-1} - \cdots - c_kt^{n-k} \]
이므로
\[ tD'(t) = nt^n - c_1(n-1)t^{n-1} - \cdots - c_k(n-k)t^{n-k} \]
를 얻는다. 한편, $C(t) = (x-r)^{m} p(t)$라는 사실로부터
\[ tD'(t) = (t-r)^{m-1} q_1(t) \quad (\text{단, $q_1(r) \neq 0$}) \]
이고 $m > 1$이므로, $rD'(r) = 0$이 됨을 알 수 있다. 따라서
\begin{align*}
0 & = rD'(t) \\[1ex]
& = nr^n - c_1(n-1)r^{n-1} - \cdots - c_k(n-k)r^{n-k}
\end{align*}
가 되어 $(nr^n)$은 점화식 $\myblue{(2.1)}$을 만족한다.
일반적으로 $1 \leq k < m$인 $k$에 대하여 \[ f_1(t) = t D'(t), \quad f_k(t) = t f'_{k-1}(t) \] 로 정의하자. 그러면 \begin{align*} f_k(t) & = n^kt^n - c_1(n-1)^kt^{n-1} - \cdots - c_k(n-k)^kt^{n-k} \\[1ex] & = (t -r)^{m-k} q_k(t) \quad (\text{단, $q_k(r) \neq 0$}) \end{align*} 를 얻는다. 이제 $m > k$이므로 $f_k(r) = 0$이다. 따라서 \[ 0 = n^kr^n - c_1(n-1)^kr^{n-1} - \cdots - c_k(n-k)^kr^{n-k} \] 가 되어 수열 $(n^kr^n)$은 점화식 $\myblue{(2.1)}$을 만족한다. - $m$개의 수열 \[ (r^n),\, (nr^n),\, (n^2r^n),\, \ldots,\, (n^{m-1}r^n) \] 이 모두 점화식 $\myblue{(2.1)}$를 만족하므로 정리 2.1.7 $\myblue{\text{(a)}}$에 의해 다음과 같이 정의된 수열 \begin{align*} c_n & = \beta_0 r^n + \beta_1 n r^n + \cdots \beta_{m-1} n^{m-1} r^n \\[1ex] & = \Big( \beta_0 + \beta_1 n + \cdots \beta_{m-1} n^{m-1} \Big) r^n \end{align*} 또한 점화식 $\myblue{(2.1)}$을 만족한다.
$ $
예제 2.1.12.
Q. 수열 $(a_n)$에 대한 점화식
\[ a_n = 4a_{n-1} - 4a_{n-2} \]
과 초기값 $a_0 = 1$, $a_1 = 4$가 주어졌을 때, 수열 $(a_n)$의 일반항을 구하여라.
A. 주어진 점화식에 대한 특성다항식은
\[ t^2 - 4t^2 + 4t = 0 \]
으로 주어지며 위 다항식은 이중근 $t = 2$를 갖는다. 따라서 정리 2.1.11에 의해 다음 수열
\[ \big( (\beta_0 + \beta_1 n)2^n \big) \]
은 주어진 점화식을 만족한다. 이제 주어진 초기조건 $a_0 = 1$, $a_1 = 0$을 $\beta_0,\, \beta_1$을 찾기 위하여 아래의 선형연립방정식
\[ \systeme[\beta_0\beta_1]{\beta_0 = 1, 2 \beta_0 + 2 \beta_1 = 4} \]
을 풀면 $\beta_0 = 1$, $\beta_1 = 1$이므로 수열 $(a_n)$의 일반항은
\[ a_n = \big( 1 + n \big)2^n. \tag*{$\myblue{\blacksquare}$} \]
$ $
예제 2.1.13.
Q. 수열 $(a_n)$에 대한 점화식
\[ a_n = 3a_{n-1} - 4a_{n-3} \]
과 초기값 $a_0 = 1$, $a_1 = 6$, $a_2 = 2$가 주어졌을 때, 수열 $(a_n)$의 일반항을 구하여라.
A. 주어진 점화식에 대한 특성다항식은
\[ t^3 - 3t^2 + 4 = 0 \]
으로 주어지며 위 다항식은 근은 $t = 2,\, 2,\, -1$이다. $t=2$가 이중근이므로 정리 2.1.8과 정리 2.1.11에 의해 다음 수열
\[ \big( (\beta_0 + \beta_1 n)2^n + \alpha (-1)^n \big) \]
은 주어진 점화식을 만족한다. 이제 주어진 초기조건 $a_0 = 1$, $a_1 = 3$, $a_2 = -5$을 만족하는 $\beta_0,\, \beta_1,\, \alpha$를 찾아보자. 다음 선형연립방정식
\[ \systeme[\beta_0\beta_1\alpha]{\beta_0 + \alpha = 1,
2 \beta_0 + 2 \beta_1 - \alpha = 6,
4 \beta_0 + 8 \beta_1 + \alpha = 2} \]
을 풀면 $\beta_0 = 3$, $\beta_1 = -1$, $\alpha = -2$이므로 수열 $(a_n)$의 일반항은
\[ a_n = (3 - n)2^n - 2 (-1)^n. \tag*{$\myblue{\blacksquare}$} \]
$ $
다음으로 비동차선형점화식을 갖는 수열 $(a_n)$의 일반항을 구하는 방법에 대하여 살펴보자.
$ $
$ $
증명.
- 두 수열 $(x_n)$과 $(q_n)$이 문제의 조건을 만족한다고 하자. 그러면 \begin{align*} x_n & = c_1 x_{n-1} + c_2 x_{n-2} + \cdots c_k x_{n-k} \\[1ex] q_n & = c_1 q_{n-1} + c_2 q_{n-2} + \cdots c_k q_{n-k} + f(n) \end{align*} 이 성립한다. 위 두 식을 더하면 \begin{align*} x_n + q_n & = \big( c_1 x_{n-1} + c_2 x_{n-2} + \cdots c_k x_{n-k} \big) \\[1ex] & \qquad + \big( c_1 q_{n-1} + c_2 q_{n-2} + \cdots c_k q_{n-k} + f(n) \big) \\[1ex] & = c_1 (x_{n-1} + q_{n-1}) + c_2 (x_{n-2} + q_{n-2}) \\[1ex] & \qquad + \cdots + c_k (x_{n-k} + q_{n-k}) + f(n) \end{align*} 이므로 수열 $(x_n + q_n)$ 또한 점화식 $\myblue{(2.3)}$을 만족한다.
- $(q_n)$이 점화식 $\myblue{(2.3)}$를 만족하는 한 특수해라 하자. 이제 $(y_n)$이 점화식 $\myblue{(2.3)}$을 만족하는 임의의 수열이라 하면 \begin{align*} y_n & = c_1 y_{n-1} + c_2 y_{n-2} + \cdots c_k y_{n-k} + f(n) \\[1ex] q_n & = c_1 q_{n-1} + c_2 q_{n-2} + \cdots c_k q_{n-k} + f(n) \end{align*} 이 성립하므로 $x_n = y_n - q_n$으로 설정하면, 수열 $(x_n)$은 동차선형점화식 부분을 만족하는 수열이면서 동시에 $y_n = x_n + q_n$이 성립한다. $ $
$ $
참고. 다음 표는 비동차항 $f(n)$에 대한 특수해 중에서 대표적인 것을 나타낸 것이다.
$ $

$ $
위의 특수해 후보가 주어진 점화식을 만족하지 않을 경우, 그 후보에 $n$ 또는 $n^2$ 등을 곱해 얻은 새로운 후보가 점화식을 만족하는지 시험해 보는 식으로 특수해를 찾을 수 있다. $ $
$ $
예제 2.1.15.
Q. 수열 $(a_n)$에 대한 점화식
\[ a_n = a_{n-1} + d \]
과 초기값 $a_1 = a$가 주어졌을 때, 수열 $(a_n)$의 일반항을 구하여라.
A. 수열 $(x_n)$이 주어진 점화식의 동차선형점화식 부분을 만족한다고 하자. 그러면 $x_n = x_{n-1}$이 성립하고, 이에 대한 특성다항식은
\[ t - 1 = 0 \]
이므로 간단히 $t = 1$이 근이 됨을 알 수 있다. 따라서 수열 $(x_n)$의 일반항은 $x_n = \alpha 1^n = \alpha$로 주어진다. 한편, 주어진 점화식을 만족하는 한 특수해 $(q_n)$을 찾기 위하여, $q_n = B_0$로 두게 되면,
\[ B = B + d \]
가 되어 이를 만족하는 $B$는 존재하지 않는다. 따라서 이번에는 $q_n = Bn$으로 추측해 보자. 그러면
\[ Bn = B(n-1) + d \]
이므로 $B = d$를 얻는다. 따라서 비동차선형점화식을 만족하는 한 특수해를 $q_n = dn$으로 둘 수 있다. 그러므로 수열
\[ (x_n + q_n) = (\alpha + dn) \]
은 주어진 점화식을 만족한다. 이제 $\alpha$의 값을 구하기 위해 초기조건 $a_1 = a$를 이용하면,
$\alpha + d = a$를 만족해야 하므로 $\alpha = a - d$임을 알 수 있다. 따라서 수열 $(a_n)$의 일반항은
\[ a_n = (a - d) + dn = a + (n-1)d. \tag*{$\myblue{\blacksquare}$} \]
$ $
예제 2.1.16.
Q. 수열 $(a_n)$에 대한 점화식
\[ a_n = n - a_{n-1} \]
과 초기값 $a_0 = 1$이 주어졌을 때, 수열 $(a_n)$의 일반항을 구하여라.
A. 수열 $(x_n)$이 주어진 점화식의 동차선형점화식 부분을 만족한다고 하자. 그러면 $x_n = -x_{n-1}$이 성립하고, 이에 대한 특성다항식
\[ t + 1 = 0 \]
의 근은 $t = -1$이므로 수열 $(x_n)$의 일반항은 $x_n = \alpha (-1)^n$이다. 한편, 주어진 점화식을 만족하는 한 특수해 $(q_n)$를 구하기 위해 $q_n = B_0 + B_1n$으로 두게 되면,
\[ B_0 + B_1n = n - (B_0 + B_1(n-1)) \]
을 얻는다. 위 식을 정리하면
\[ (2B_1 - 1)n + (2B_0 - B_1) = 0 \]
이므로 $B_1 = \frac{1}{2},\, B_0 = \frac{1}{4}$을 얻는다. 따라서 비동차선형점화식을 만족하는 한 특수해를 $q_n = \frac{1}{4} + \frac{1}{2}n$으로 둘 수 있다. 그러므로 수열
\[ x_n + q_n = \alpha (-1)^n + \frac{1}{4} + \frac{1}{2}n \]
은 주어진 점화식을 만족한다. 이제 $\alpha$의 값을 구하기 위해 초기조건 $a_0 = 1$을 이용하면, $n = 0$일 때,
\[ \alpha + \frac{1}{4} = 1 \]
이므로 $\alpha = \frac{3}{4}$이다. 따라서 수열 $(a_n)$의 일반항은
\[ a_n = \frac{3}{4} (-1)^n + \frac{1}{4} + \frac{1}{2} n = \frac{1}{4} \big( 3(-1)^n + 1 + 2n \big). \tag*{$\myblue{\blacksquare}$} \]
$ $
예제 2.1.17.
Q. 다음 수열 $(a_n)$에 대한 점화식과 초기조건을 이용하여 일반항을 구하여라.
- $a_n = 3a_{n-1} + 2^n$, $a_0 = 1$
- $a_n = 3a_{n-1} + 3^n$, $a_0 = 1$
A.
- 위 점화식의 동차선형점화식 부분인 $a_n = 3a_{n-1}$의 특성다항식은 $C(t) = t - 3 = 0$이고 그 근은 $t = 3$이므로 동차선형점화식을 만족하는 일반해를 $x_n = \alpha 3^{n}$으로 둘 수 있다. 이제 위 점화식의 한 특수해를 $q_n = B2^n$으로 두면 \[ B2^n = 3B2^{n-1} + 2^n \] 이므로, 위 식을 풀면 $B = -2$이고 따라서 $q_n = -2^{n+1}$이다. 그러므로 \[ x_n + q_n = \alpha 3^n - 2^{n+1} \] 은 주어진 점화식을 만족한다. 이제 $\alpha$의 값을 구하기 위해 초기조건 $a_0 = 1$을 이용하면 $\alpha = 3$을 얻는다. 따라서 수열 $(a_n)$의 일반항은 \[ a_n = 3^{n+1} - 2^{n+1}. \]
- 문제 $\myblue{\text{(a)}}$와 마찬가지로 동차선형점화식을 만족하는 일반해를 $x_n = \alpha 3^{n}$으로 둘 수 있다. 이제 위 점화식의 한 특수해를 $q_n = B3^n$으로 두게 되면, 일반해인 $(x_n)$과 특수해인 $(q_n)$의 형태가 같아지게 되어 비동차점화식의 일반해를 구할 수 없다. 따라서 $q_n = Bn3^n$으로 두자. 이제 $q_n$을 주어진 점화식에 대입하면 \[ Bn3^n = 3B(n-1)3^{n-1} + 3^n \] 이므로 위 방정식을 풀어 $B = 1$을 얻는다. 따라서 \[ x_n + q_n = \alpha 3^n + n3^n \] 은 주어진 점화식을 만족한다. 이제 $\alpha$의 값을 구하기 위해 초기조건 $a_0 = 1$을 이용하면 $\alpha = 1$이므로, 수열 $(a_n)$의 일반항은 \[ a_n = 3^{n} + n3^{n} = (n+1)3^n. \tag*{$\myblue{\blacksquare}$} \]
$ $
수열 $(a_n)$의 점화식이 비선형인 경우에는 위에서 살펴본 방법을 직접 적용할 수 없다. 하지만 다음과 같이 몇몇 특수한 경우에는 치환을 통해 주어진 비선형방정식을 선형방정식으로 변환할 수 있다.
$ $
예제 2.1.17.
Q. 다음 수열 $(a_n)$에 대한 점화식과 초기조건을 이용하여 일반항을 구하여라.
- $(n+1)a_n + (n-1)a_n + 2 = 0$
- $a_n = \sqrt{a_{n-1} a_{n-2}}$ (단, $a_n > 0$)
- $a_n = \dfrac{a_{n-1}}{2 + a_{n-1}}$
- $a_n = na_{n-1}$
A.
- 주어진 점화식의 양변에 $n$을 곱해주면 \[ n(n+1)a_n + (n-1)na_n + 2n = 0 \] 따라서 $b_n = n(n+1)a_n$으로 치환하면 \[ b_n + b_{n-1} + 2n = 0 \] 형태의 (비동차)선형점화식을 얻는다.
- 주어진 점화식의 양변에 $\log_2$를 취한 뒤, $b_n = \log_2(a_n)$으로 치환하면 \[ b_n = b_{n-1} + b_{n-2} \] 가 된다.
- 주어진 점화식의 양변에 역수를 취하고 정리하면 \[ \frac{1}{a_n} = \frac{2 + a_{n-1}}{a_{n-1}} = \frac{2}{a_{n-1}} + 1 \] 따라서 $b_n = \dfrac{1}{a_n}$으로 치환하여 선형점화식 \[ b_n = 2b_{n-1} + 1 \] 을 얻는다.
- $b_n = \dfrac{a_n}{n!}$로 치환하면 \[ n!b_n = n (n-1)! b_{n-1} \] 따라서 양변을 $n!$으로 나누면 선형점화식 $b_n = b_{n-1}$을 얻는다. $ $
$ $