$ $
예제 1.3.2.
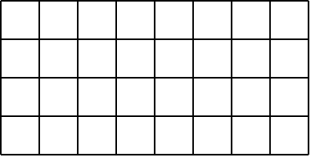
Q. 다음 도형에 있는 직사각형의 개수와 정사각형의 개수를 각각 구하여라.
$ $
$ $
A. $2$개의 세로선과 $2$개의 가로선을 택하면 직사각형이 유일하게 결정된다. 위 도형에서 세로선은 총 $9$개, 가로선은 총 $5$개 존재하므로 \[ \binom{9}{2} \binom{5}{2} = 30. \] 크기가 각각 $1,\, 4,\, 9,\, 16$인 정사각형으로 경우를 나누어 생각하면 \[ 8 \cdot 4 + 7 \cdot 3 + 6 \cdot 2 + 5 \cdot 1 = 70. \tag*{$\myblue{\blacksquare}$}\]
$ $
예제 1.3.3.
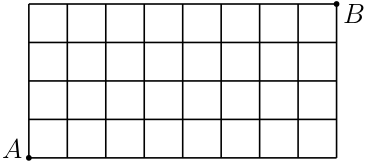
Q. 다음 도형에 있는 직사각형의 개수와 정사각형의 개수를 각각 구하여라.
$ $
$ $
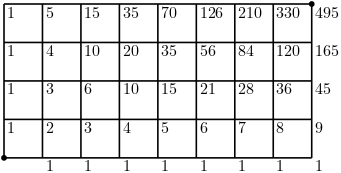
A1. $A$-지점에서 $B$-지점으로 최단 경로로 도달하기 위해서는 오른쪽으로 $8$번, 위쪽으로 $4$번 이동해야 한다. 이는 총 $8+4=12$번의 이동 중 언제 오른쪽으로 $8$번 이동할지를 결정하는 것과 같으므로 원하는 경우의 수는 \[ \binom{12}{8} = 495. \tag*{$\myblue{\blacksquare}$} \] A2. 다음과 같이 합의 법칙을 이용하여 전체 경우의 수를 구할 수 있다.
$ $
$ $
$ $
참고. 일반적으로 $m \times n$ 크기의 격자 모양의 도로망에의 왼쪽 아래 끝점에서 오른쪽 위 끝점에 이르는 최단 경로의 수는 \[ \binom{m+n}{m} = \binom{m+n}{n} \] 과 같다. $ $
$ $
다음은 조합을 포함하는 등식을 조합론적으로 증명한 예들이다.
$ $
$ $
증명.
- $n$명의 지원자 중에서 $r$명의 합격자를 선택하는 경우의 수 $\binom{n}{r}$은 $n$명의 지원자 중에서 $n-r$명의 불합격자를 선택하는 경우의 수 $\binom{n}{n-r}$과 같다.
- $n$명의 지원자 중에서 $r$명의 합격자를 선택하는 경우의 수 $\binom{n}{r}$은 $n$명의 지원자중에서 $a$라는 지원자를 먼저 합격 시키고 나머지 $n-1$명의 지원자 중에서 $r-1$명의 합격자를 선택하는 경우의 수 $\binom{n-1}{r-1}$과 $n$명의 지원자 중 $a$는 불합격 시키고 나머지 $n-1$명 중에서 $r$명의 합격자를 선택하는 경우의 수 $\binom{n-1}{r}$의 합과 같다.
- $n$명의 지원자 중에서 $r$명의 합격자를 선택하고, 이 합격자들 $r$명 중에서 합격자 대표를 한명 선출하는 경우의 수 $r\binom{n}{r}$은, $n$명의 지원자 중에서 합격자 대표를 먼저 선택하고, 나머지 $n-1$명의 지원자 중에서 $r-1$명의 합격자를 선택하는 경우의 수 $n \binom{n-1}{r-1}$과 같다.
- $n$명의 지원자 중에서 $r$명의 합격자를 선택하고, 이 합격자들 $r$명 중에서 합격자 대표를 한명 선출하는 경우의 수 $r\binom{n}{r}$은, $n$명의 지원자 중에서 합격자 대표가 될 사람을 제외한 $r-1$명의 합격자만을 먼저 선택하고, 나머지 $n-(r-1)$명 중에서 합격자 대표를 선출하는 경우의 수 $(n-r+1) \binom{n}{r-1}$과 같다.
- 위 식의 좌변은 $n$명의 지원자 중에서 임의의 $0 \leq k \leq n$에 대하여, $k$명의 합격자를 선택하는 경우의 수와 같다. 이 때, 모든 $k$를 고려하므로 각각의 지원자는 합격했을 수도 또는 불합격했을 수도 있다. 따라서 이는 각각의 지원자 $n$명에게 개별적으로 합격, 또는 불합격을 통보하는 경우의 수 $2^n$과 같다.
- 위 식의 좌변은 $n$명의 지원자 중에서 임의의 $0 \leq k \leq n$에 대하여, $k$명의 합격자를 선택하고, 이 합격자들 $k$명 중에서 합격자 대표를 한명 선출하는 경우의 수와 같다. 이는 우선 $n$명의 지원자들 중에서 합격자 대표를 먼저 선출하고, 나머지 $n-1$명에서 개별적으로 합격, 또는 불합격을 통보하는 경우의 수 $n2^{n-1}$과 같다.$ $
$ $
$ $
예제 1.3.6.
Q. $n$이 음이 아닌 정수일 때, 카탈란 수 $C_n$은 정수임을 보여라.
A. 정리 1.3.4 $\myblue{\text{(d)}}$에 의해
\[ \binom{2n}{n+1} = \frac{n}{n+1} \binom{2n}{n} \]
을 얻는다. 따라서
\[ C_n = \frac{1}{n+1} \binom{2n}{n} = \binom{2n}{n} - \frac{n}{n+1} \binom{2n}{n} = \binom{2n}{n} - \binom{2n}{n+1} \]
$\binom{2n}{n}$, $\binom{2n}{n+1}$은 모두 정수이므로, $C_n$ 또한 정수임을 알 수 있다. $ $
카탈란 수는 조합론에서 빈번하게 등장하는 수 중의 하나로, 아래와 같은 문제들의 해답이 모두 $n$번째 카탈란 수 $C_n$으로 주어진다. 먼저 $C_4 = 14$라는 사실을 기억하자.
- $C_n$은 $n$쌍의 여는 괄호 `('와 닫는 괄호 `)'로 만들 수 있는 올바른 괄호 구조의 경우의 수와 같다. 예를 들어 $4$쌍의 열린 괄호와 닫는 괄호로는 아래의 $14$가지 경우의 수가 나온다. \begin{align*} & (((()))) \quad (())(()) \quad (()()()) \quad ()((())) \quad ()(()()) \\[1ex] & ()()(()) \quad (()(())) \quad ()()()() \quad ((()())) \quad ()(())() \\[1ex] & ((()))() \quad (()())() \quad (())()() \quad ((())()) \end{align*}
- $C_n$은 $(n+1)$개의 항에 이항연산을 적용하는 순서의 가짓수와 같다. 예를 들어 $5$개의 문자 $a,\, b,\, c,\, d,\, e$에 괄호로 이항연산의 순서를 표현하면 아래의 $14$가지 경우가 나온다. \begin{align*} & (((ab)c)d)e \quad ((ab)(cd))e \quad (ab)((cd)e) \quad ((ab)c)(de) \\[1ex] & a(b(c(de))) \quad a((bc)(de)) \quad (a(bc))(de) \quad (ab)(c(de)) \\[1ex] & ((a(bc))d)e \quad (a((bc)d))e \quad a(((bc)d)e) \\[1ex] & a(b((cd)e)) \quad a((b(cd))e) \quad (a(b(cd)))e \end{align*}
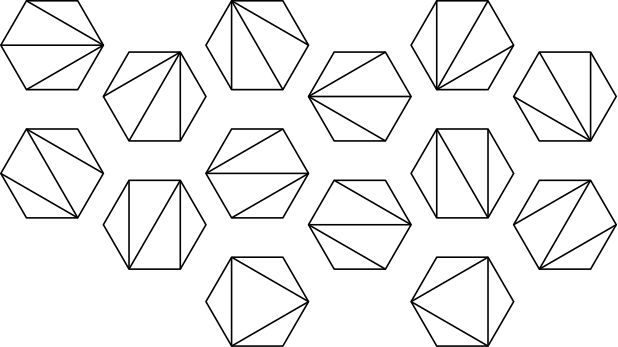
- $C_n$은 $(n+2)$각형을 $n$개의 삼각형으로 나누는 방법의 개수이다. 아래 그림은 $6$각형을 $4$개의 삼각형으로 나누는 $14$가지 경우를 모두 나타낸 것이다.
$ $
$ $
- $C_n$은 $(n+2)$각형을 $n$개의 삼각형으로 나누는 방법의 개수이다. 아래 그림은 $6$각형을 $4$개의 삼각형으로 나누는 $14$가지 경우를 모두 나타낸 것이다.
$ $

$ $
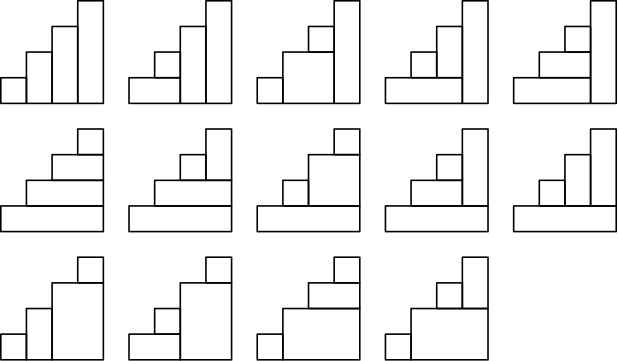
- $C_n$은 $(n+2)$각형을 $n$개의 삼각형으로 나누는 방법의 개수이다. 아래 그림은 $6$각형을 $4$개의 삼각형으로 나누는 $14$가지 경우를 모두 나타낸 것이다.
$ $
$ $
- $C_n$은 $(n+2)$각형을 $n$개의 삼각형으로 나누는 방법의 개수이다. 아래 그림은 $6$각형을 $4$개의 삼각형으로 나누는 $14$가지 경우를 모두 나타낸 것이다.
$ $

$ $
$ $
$ $
예제 1.3.8.
Q. 방정식 $x + y + z = 10$에 대하여 다음을 구하여라.
- 음이 아닌 정수해 $(x,\, y,\, z)$의 개수
- $x,\, y,\, z \geq 2$를 만족하는 정수해 $(x,\, y,\, z)$의 개수
- $x$는 홀수, $y$는 짝수인 음이 아닌 정수해 $(x,\, y,\, z)$의 개수
A.
- 위 문제는 세 문자 $x,\, y,\, z$를 중복을 허락하여 $10$개를 선택하는 경우의 수와 같으므로 \[ {}_{3}H_{10} = \binom{12}{10} = \binom{12}{2} = 66. \]
- $x=X+2$, $y=Y+2$, $z=Z+2$로 치환하여 정리한 방정식 \[ X + Y + Z = 4 \] 의 음이 아닌 정수해 $(X,\, Y,\, Z)$는 원래 방정식의 $x,\, y,\, z \geq 2$를 만족하는 정수해 $(x,\, y,\, z)$와 일대일대응 관계를 이룬다. 따라서 \[ {}_{3}H_{4} = \binom{6}{4} = \binom{6}{2} = 15. \]
- $x=2X+1$, $y=2Y$, $Z=z$로 치환하여 정리한 방정식 \[ 2X + 2Y + Z = 9 \] 의 음이 아닌 정수해 $(X,\, Y,\, Z)$는 원래 방정식의 주어진 조건을 만족하는 정수해 $(x,\, y,\, z)$와 일대일대응 관계를 이룬다. 위 방정식 좌변의 $2X + 2Y$는 짝수이므로 위 식의 정수해가 존재하기 위해서는 $Z = 1,\, 3,\, 5,\, 7,\, 9$가 되어야 한다. 예를 들어 $Z = 1$인 경우 방정식 $X + Y = 4$의 음이 아닌 정수해를 구하면 충분하므로, 구하는 경우의 수는 ${}_{2}H_{4}$가 된다. 마찬가지 방법으로 모든 경우의 수를 구하면 \begin{align*} & {}_{2}H_{4} + {}_{2}H_{3} + {}_{2}H_{2} + {}_{2}H_{1} + {}_{2}H_{0} \\[1ex] & \qquad = \binom{5}{4} + \binom{4}{3} + \binom{3}{2} + \binom{2}{1} + \binom{1}{0} \\[1ex] & \qquad = 15. \tag*{$\myblue{\blacksquare}$} \end{align*}
$ $
예제 1.3.9.
Q. 부등식 $x + y + z \leq 10$에 대하여 다음을 구하여라.
- 음이 아닌 정수해 $(x,\, y,\, z)$의 개수
- 양의 정수해 $(x,\, y,\, z)$의 개수
A.
- 새로운 변수 \[ w = 10 - (x + y + z) \] 를 정의하자. 그러면 $(x,\, y,\, z)$가 주어진 부등식의 음이 아닌 정수해인 것과 $(w,\, x,\, y,\, z)$가 다음 방정식 \[ w + x + y + z = 10 \] 의 음이 아닌 정수해인 것은 서로 동치이다. 그러므로 위 부등식과 방정식의 음이 아닌 정수해의 개수는 서로 같으므로, \[ {}_{4}H_{10} = {}_{13}C_{10} = 858. \]
- 위와 같은 방법으로 $w$를 정의하자. 그러면 $(x,\, y,\, z)$가 주어진 부등식의 양의 정수해인 것과 $(w,\, x,\, y,\, z)$가 다음 방정식 \[ w + x + y + z = 10 \] 에서 $x,\, y,\, z > 0$이고 $w \geq 0$를 만족하는 정수해인 것은 서로 동치이다. 또한 이 조건들을 만족하는 방정식의 정수해의 개수는 $x=X+1$, $y=Y+1$, $z=Z+1$로 치환하여 정리한 방정식 \[ w + X + Y + Z = 7 \] 의 음이 아닌 정수해 $(w,\, X,\, Y,\, Z)$의 개수와 같다. 그러므로 \[ {}_{4}H_{7} = {}_{10}C_{7} = 120. \tag*{$\myblue{\blacksquare}$} \]
$ $