예제 1.5.1
Q. $5$를 $2+2+1$과 같이 몇 개의 양의 정수의 합으로 나타내는 방법은 모두 몇 가지인가? 단 합의 순서가 다르면 다른 것으로 간주한다.
A. 직접 구해보면 \[ \begin{array}{lllll} 5 & \phantom{xxx} & 3+1+1 & \phantom{xxx} & 2+1+1+1 \\ 4+1 & \phantom{xxx} & 2+2+1 & \phantom{xxx} & 1+2+1+1 \\ 3+2 & \phantom{xxx} & 2+1+2 & \phantom{xxx} & 1+1+2+1 \\ 2+3 & \phantom{xxx} & 1+3+1 & \phantom{xxx} & 1+1+1+2 \\ 1+4 & \phantom{xxx} & 1+2+2 & \phantom{xxx} & 1+1+1+1+1 \\ & \phantom{xxx} & 1+1+3 & \phantom{xxx} & \end{array} \] 이 되어 모두 $16$가지임을 알 수 있다. $ $

$ $

정의 1.5.2 합성_{(composition)}

양의 정수 $n$에 대하여 \[ n = n_1 + n_2 + \cdots + n_k \] 을 만족하는 양의 정수의 순서쌍 $\lambda = (n_1,\, n_2,\, \ldots,\, n_k)$를 $n$의 합성_{(composition)}이라 한다.

$ $

$n$의 모든 합성의 개수를 $c(n)$으로 나타내고, $k$개의 부분을 가진 $n$의 합성의 개수를 $c(n,\, k)$로 나타낸다. 그러므로 정의에 의해 \[ \begin{align*} c(n) & = \sum_{k=1}^{n} c(n,\, k) \\[1ex] & = c(n,\, 1) + c(n,\, 2) + \cdots + c(n,\, n) \end{align*} \] 이 성립한다. 이제 $n \geq k$에 대하여 $c(n,\, k)$의 값을 구해보자. 이는 방정식 \[ x_1 + x_2 + \cdots + x_k = n \] 의 양의 정수해의 개수와 같으므로, \[ {}_{k}H_{n-k} = \binom{n-1}{n-k} = \binom{n-1}{k-1} \] 이다. 따라서 \[ c(n) = \sum_{k=1}^{n} c(n,\, k) = \sum_{k=1}^{n} \binom{n-1}{k-1} = 2^{n-1} \] 를 얻는다.

$ $

예제 1.5.3
Q. $6$을 $3+2+1$과 같이 몇 개의 양의 정수의 합으로 나타내는 방법은 모두 몇 가지인가? 단 합의 순서만 다른 것은 모두 같은 것으로 간주한다.
A. 직접 구해보면 \[ \begin{array}{lll} 6 & \phantom{xxx} & 3+1+1+1 \\ 5+1 & \phantom{xxx} & 2+2+2 \\ 4+2 & \phantom{xxx} & 2+2+1+1 \\ 4+1+1 & \phantom{xxx} & 2+1+1+1+1 \\ 3+3 & \phantom{xxx} & 1+1+1+1+1+1 \\ 3+2+1 & \phantom{xxx} & \end{array} \] 이 되어 모두 $11$가지임을 알 수 있다. $ $

$ $

정의 1.5.4 분할_(partition)

양의 정수 $n$에 대하여 다음 두 조건을 만족하는 양의 정수의 순서쌍 $\lambda = (n_1,\, n_2,\, \ldots,\, n_k)$를 $n$의 분할_(partition)이라 한다.

1. $n = n_1 + n_2 + \cdots + n_k$
2. $n_1 \geq n_2 \geq \cdots \geq n_k$

만약 $\lambda = (n_1,\, n_2,\, \ldots,\, n_k)$가 $n$의 분할이면 $\lambda \vdash n$으로 나타낸다.

$ $

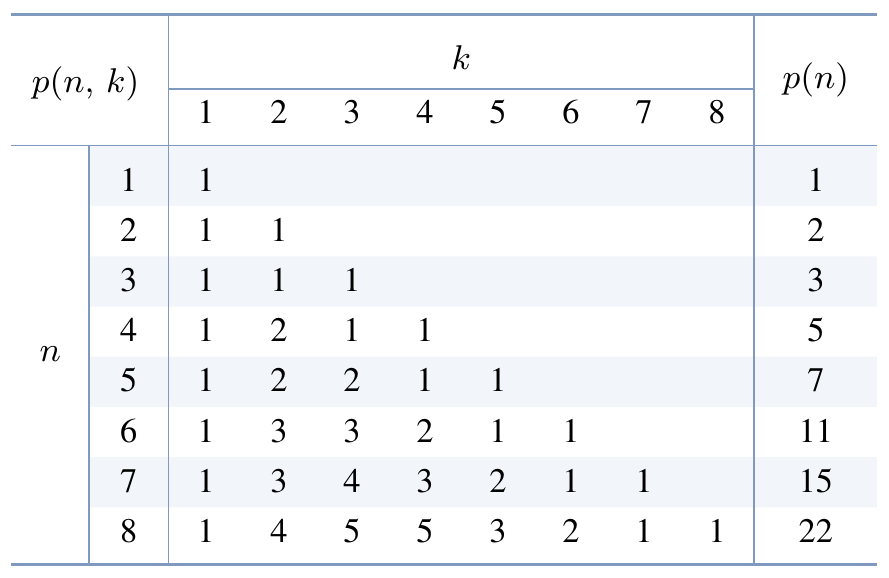
$n$의 모든 분할의 개수를 $p(n)$으로 나타내고 $n$에 대한 분할수_{(partition number)}라 한다. 또한 $k$개의 부분을 가진 $n$의 분할의 개수를 $p(n,\, k)$로 나타낸다. 그러므로 정의에 의해 \begin{align*} p(n) & = \sum_{k=1}^{n} p(n,\, k) \\[1ex] & = p(n,\, 1) + p(n,\, 2) + \cdots + p(n,\, n) \end{align*} 이 성립한다. 위의 예제 1.5.3에서 \[ p(6) = 11, \quad p(6, 2) = 3, \quad p(6,\, 4) = 2 \] 와 같은 식이다.

$ $

$n = 1,\ 2,\, 3,\, \ldots$일 때, $p(n)$의 값을 계산해 보면 \[ 1,\, 2,\, 3,\, 5,\, 7,\, 11,\, 15,\, 22,\, 30,\, 42,\, \ldots \] 의 수열을 얻을 수 있지만, 이 수열의 $n$에 대한 일반항 또는 점화식 모두 현재까지 알려져 있지 않다.

$ $

예제 1.5.5
Q. $10$개의 같은 종류의 공과 $3$개의 같은 종류의 상자가 있다고 하자. 이때, 다음을 각각 구하여라.

1. 빈 상자가 없도록 상자에 공을 넣는 방법의 수
2. 상자에 공을 넣는 방법의 수
3. 모든 상자에 $2$개 이상의 공이 있도록 상자에 공을 넣는 방법의 수

A.

1. 전체 방법의 수는 $3$개의 부분을 가진 $10$의 분할과 같다. 따라서 \[ p(10,\, 3) = 8. \]
2. 빈 상자가 있을 수도 있으므로 전체 방법의 수는 많아야 $3$개의 부분을 가진 $10$의 분할과 같다. 따라서 \[ p(10,\, 1) + p(10,\, 2) + p(10,\, 3) = 1 + 5 + 8 = 14. \]
3. 먼저 $4$개의 공을 $3$개의 상자에 넣은 후에, 나머지 $6$개의 공을 각 상자에 $2$개씩 넣으면 모든 상자에는 $2$개 이상의 공이 들어가게 된다. 따라서 \[ p(4,\, 1) + p(4,\, 2) + p(4,\, 3) = 1 + 2 + 1 = 4. \] 또는 먼저 $7$개의 공을 빈 상자가 없도록 $3$개의 상자에 넣은 후에, 나머지 $3$개의 공을 각 상자에 $1$개씩 넣으면 모든 상자에는 $2$개 이상의 공이 들어가게 된다. 따라서 \[ p(7,\, 3) = 4. \tag*{$\myblue{\blacksquare}$} \]

$ $

참고. 위 예제 1.5.5.의 결과를 일반화하면 다음 결과를 얻는다: 양의 정수 $n \geq k$에 대하여, \[ \sum_{j=1}^{k} p(n,\, j) = p(n+k,\, k) \] 를 얻는다. 특히, $n = k$인 경우, \[ p(n) = \sum_{j=1}^{n} p(n,\, j) = p(2n,\, n). \tag*{$\myblue{\square}$} \]

$ $

예제 1.5.6
Q. 다음 방정식 \[ x + y + z = 6 \] 을 만족하고 $x \geq y \geq z$인

1. 양의 정수해 $(x,\, y,\, z)$의 개수
2. 음이 아닌 정수해 $(x,\, y,\, z)$의 개수

를 각각 구하여라.
A.

1. 부분의 개수가 $3$개인 $6$의 분할의 개수와 같으므로 $p(6,\, 3) = 3$.
2. 부분의 개수가 $3$개 이하인 $6$의 분할의 개수와 같으므로 \[ p(6,\, 1) + p(6,\, 2) + p(6,\, 3) = 1 + 3 + 3 = 7. \tag*{$\myblue{\blacksquare}$} \]

$ $

참고. 일반적으로 양의 정수 $n \geq k$에 대하여, 방정식 \[ x_1 + x_2 + \cdots + x_k = n \] 을 만족하는 양의 정수개의 개수는 $p(n,\, k)$와 같고, 음이 아닌 정수해의 개수는 \[ \sum_{i=1}^{k} p(n,\, i) \] 와 같다. $ $

$ $

정의 1.5.7 분할수에 대한 점화식

$n \geq k$인 양의 정수 $n,\, k$에 대하여 \[ p(n,\, k) = p(n-1,\, k-1) + p(n-k, k). \]

$ $

증명. 부분의 개수가 $k$개인 $n$의 분할 $\lambda = (n_1,\, n_2,\, \ldots,\, n_k)$ 의 개수 $p(n,\, k)$를 다음 두가지 경우로 나누어 계산하자.

• $\lambda$가 $1$을 포함하지 않는 경우: 이 경우, 모든 부분의 크기가 $2$ 이상이므로, \[ \mu = \big( n_1 - 1,\, n_2 - 1,\, \ldots,\, n_k - 1 \big) \] 은 부분의 개수가 $k$개인 $n-k$에 대한 한 분할이 된다. 이 과정은 일대일대응이므로, $1$을 포함하지 않는 부분의 개수가 $k$개인 $n$의 분할의 개수는 \[ p(n-k,\, k) \]
• $\lambda$가 $1$을 적어도 $1$개 포함하는 경우: 이 경우, $n_k = 1$이므로, \[ \mu = \big( n_1,\, n_2,\, \ldots,\, n_{k-1} \big) \] 는 부분의 개수가 $k-1$개인 $n-1$의 한 분할이 된다. 이 과정은 일대일대응이므로, $1$을 적어도 하나 포함하는 부분의 개수가 $k$개인 $n$의 분할의 개수는 \[ p(n-1,\, k-1) \]

위 두 경우는 동시에 일어나지 않으므로, \[ p(n,\, k) = p(n-1,\, k-1) + p(n-k, k) \] 를 얻는다. $ $

$ $

위 정리를 이용하여 $p(n)$의 값을 구해보면

$ $

$ $

페러스 그림은 양의 정수의 분할을 시각적으로 도식화하고 이를 이용하여 분할에 관한 항등식 등을 증명하는 도구로 자주 쓰인다.

$ $

정의 1.5.8 페러스 그림_{(Ferrers diagram)}

$\lambda = (n_1,\, n_2,\, \ldots,\, n_k)$가 $n$의 분할이라 하자. 이 때, $i$번째 행에 $n_i$개의 정사각형을 일렬로 늘어 놓은 형태의 그림을 페러스 그림_{(Ferrers diagram)} 또는 영 그림_{(Young diagram)}이라 한다.

$ $

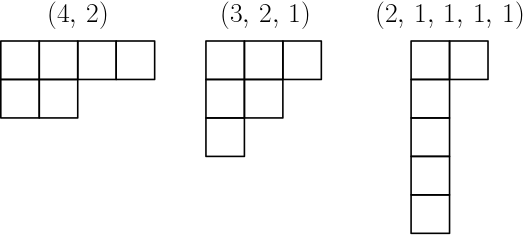
위 예제 1.5.3에서 $(4,\, 2),\, (3,\, 2,\, 1),\, (2,\, 1,\, 1,\, 1,\, 1) \vdash 6$임을 확인하였다. 이제 위 $3$가지 분할에 대한 페러스 그림을 각각 그려보면

$ $

$ $

를 얻는다.

$ $

이제 분할 $\lambda \vdash n$에 해당하는 페러스 그림을 주대각선을 기준으로 대칭하면 새로운 $n$에 대한 페러스 그림을 얻게 되는데, 이 대칭된 페러스 그림에 해당되는 분할을 $\lambda'$으로 나타내고 이를 $\lambda$의 켤레분할_{(conjugate partition)}이라 한다. 예를 들어, 위에서 살펴본 $6$에 대한 세 분할 $(4,\, 2),\, (3,\, 2,\, 1),\, (2,\, 1,\, 1,\, 1,\, 1)$에 대한 켤레분할을 각각 구해보면

$ $

$ $

특히 분할 $(3,\, 2,\, 1)$의 경우 켤레분할이 자기 자신과 같음을 알 수 있는데, 이와 같이 어떤 분할 $\lambda \vdash n$에 대하여 $\lambda' = \lambda$가 성립하는 경우, $\lambda$를 자기켤레_{(self conjugate)}라 한다.

$ $

정리 1.5.9

양의 정수 $n$에 대하여 다음이 성립한다.

1. 각 부분의 크기가 $m$ 이하인 $n$의 분할의 수는, 부분의 개수가 $m$개 이하인 $n$의 분할의 수와 같다.
2. 각 부분이 서로 다른 홀수인 $n$의 분할의 수는, 자기켤레인 $n$의 분할의 수와 같다.
3. 각 부분이 짝수인 $n$의 분할의 수는, 크기가 같은 부분의 개수가 모두 짝수인 $n$의 분할의 수와 같다.
4. (분할에 대한 오일러의 정리) 각 부분이 홀수인 $n$의 분할의 수는, 각 부분이 서로 다른 $n$의 분할의 수와 같다.

$ $

증명.

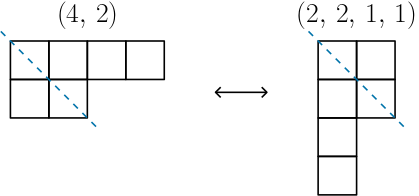
1. $n$의 한 분할 $\lambda \vdash n$의 의 가장 큰 부분의 크기가 $m$ 이라 가정하자. 그러면 켤레분할 $\lambda'$의 부분의 개수는 $m$개가 된다. 예를 들어 $(4,\, 2) \vdash 6$의 경우 가장 큰 부분의 크기가 $4$이고

   $ $

   

   $ $

   $(4,\, 2)' = (2,\, 2,\, 1,\, 1)$의 경우 부분의 개수가 $4$개가 된다. 이와 같이 두 대상 사이에 일대일대응 관계를 줄 수 있으므로 주어진 명제가 성립한다.

2. 각 부분이 서로 다른 홀수인 $n$의 분할 $\lambda \vdash n$와 자기켤레인 $n$의 분할 $\mu \vdash n$ 사이에 아래와 같은 대응관계를 줄 수 있다.

   $ $

   

   $ $

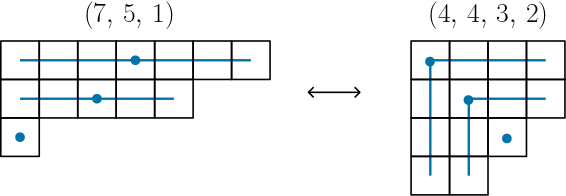
   위 대응관계는 일대일대응이므로 주어진 명제가 성립한다.

3. 아래 페러스 그림과 같이

   $ $

   

   $ $

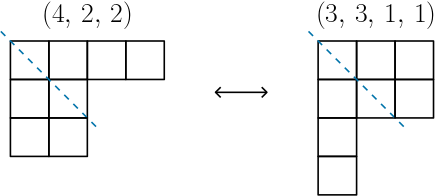
   각 부분이 짝수인 $n$의 분할 $\lambda$의 켤레분할 $\lambda'$는 언제나 크기가 같은 부분의 개수가 모두 짝수인 $n$의 분할이 된다.

4. 링크 참고. $ $

$ $

정리 1.5.10

양의 정수 $n$에 대하여 방정식 \[ x_1 + 2x_2 + 3x_3 + \cdots nx_n = n \] 의 음이 아닌 정수해 $(x_1,\, x_2,\, \ldots,\, x_n)$의 개수는 $n$의 분할의 수와 같다.

$ $

증명. $n$의 한 분할 $\lambda \vdash n$이 주어졌다고 하자. 이제 $1 \leq k \leq n$에 대하여, $\lambda$의 크기가 $k$인 분할의 개수를 $x_k$로 정의하자. 그러면 $(x_1,\, x_2,\, \ldots,\, x_n)$는 주어진 방정식의 음이 아닌 정수해가 된다.

예를 들어 $(2,\, 1,\, 1,\, 1) \vdash 5$의 경우 크기가 $1$인 부분이 $3$개 있으므로 $x_1 = 3$, 크기가 $2$인 부분이 $1$개 있으므로 $x_2 = 1$, 그리고 $x_3 = x_4 = x_5 = 0$이 된다. 그러면 $(3,\, 2,\, 0,\, 0,\, 0)$이 위 방정식에서 $n=5$일 때의 음이 아닌 정수해임을 쉽게 확인할 수 있다.

위와 같은 대응관계는 일대일대응임은 간단히 확인할 수 있고, 따라서 주어진 명제가 성립한다. $ $

$ $

예제 1.5.11
Q. 분할을 이용하여 다음을 각각 구하여라.

1. 방정식 \[ x_1 + 2x_2 + 3x_3 + 4x_4 + 5x_5 + 6x_6 = 6 \] 의 음이 아닌 정수해 $(x_1,\, x_2,\, \ldots,\, x_6)$의 개수
2. 방정식 \[ x_1 + 2x_2 + 3x_3 = 6 \] 의 음이 아닌 정수해 $(x_1,\, x_2,\, \ldots,\, x_6)$의 개수

A.

1. 위의 정리 1.5.9$\myblue{\text{(a)}}$에 의해 $p(6) = 11$.
2. 위 방정식의 음이 아닌 정수해의 개수는 각 부분의 크기가 $3$ 이하인 $6$의 분할의 개수와 같다. 또한 이 개수는 \emph{정리 \ref{thm:partition}(a)}에 의해 부분의 개수가 $3$개 이하인 $6$의 분할의 개수와 같다. 따라서 \[ p(6,\, 1) + p(6,\, 2) + p(6,\, 3) = 1 + 3 + 3 = 7. \tag*{$\myblue{\blacksquare}$} \]

$ $