비둘기집의 원리_{(pigeonhole principle)}, 또는 디리클레 상자 원리_{(Dirichlet's box principle)}라고도 불리는 정리는 $n+1$개의 공을 $n$개의 상자에 담는 경우, 최소한 한 상자에는 반드시 두 개 이상의 공이 들어가게 된다는 내용을 담고 있다. 이 원리를 수학적으로 기술하면 다음과 같다.

$ $

정리 1.8.1. 비둘기집의 원리_{(pigeonhole principle)}

두 집합 $X,\, Y$에 대하여 $\abs{X} > \abs{Y}$라 가정하자. 그러면 임의의 함수 $f : X \to Y$에 대하여, $\abs{f^{-1}(\{y\})} \geq 2$를 만족하는 $y \in Y$가 적어도 하나 존재한다.

$ $

증명. 결론에 반하여, 모든 $y \in Y$에 대하여 $\abs{f^{-1}(\{y\})} < 2$라 가정해보자. 그러면 $\abs{f^{-1}(\{y\})} \leq 1$이 성립하므로 \[ \abs{X} = \sum_{y \in Y} \abs{f^{-1}(\{y\})} \leq \sum_{y \in Y} 1 = \abs{Y} \] 이 되어 모순이다. 따라서 $\abs{f^{-1}(\{y\})} \geq 2$를 만족하는 $y \in Y$가 적어도 하나 존재한다. $ $

$ $

참고. 비둘기집의 원리는 '두 집합 $X,\, Y$에 대하여 $\abs{X} > \abs{Y}$를 만족하는 단사함수 $f : X \to Y$는 존재하지 않는다'로 이해할 수 있다. $ $

$ $

예제 1.8.2.
Q. 한 편의 길이가 $3$인 정사각형의 내부에 $10$개의 점을 임의의 잡으면 그 중에는 거리가 $\sqrt{2}$ 이하인 두 점이 반드시 존재함을 보여라.
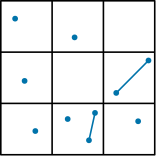
A. 다음과 같이 주어진 정사각형을 한 편의 길이가 $1$인 $9$개의 작은 정사각형으로 나누어 보자.

$ $

$ $

그러면 비둘기집의 원리에 의해 점을 $2$개 이상 포함하는 정사각형이 반드시 존재하고 이 정사각형 안에 있는 두 점은 거리가 $\sqrt{2}$ 이하여야만 한다. $ $

$ $

예제 1.8.3.
Q. 집합 $A = \{1,\, 2,\, \ldots,\, 2n\}$에서 원소의 개수가 $n+1$인 부분집합 $B$를 임의로 택할 때, 서로소인 $B$의 원소 두 개를 언제나 택할 수 있음을 보여라.
A. 다음과 같은 $n$개의 $A$의 부분집합들을 생각하자. \[ \{1,\, 2\},\, \{3,\, 4\},\, \ldots,\, \{2n-1,\, 2n\}. \] 그러면 비둘기집의 원리에 의해 원소의 개수가 $n+1$인 부분집합 $B$는 위 부분집합들 중 하나를 적어도 하나 포함해야 하며, 그 부분집합에 속한 두 원소는 서로소이다. $ $

$ $

예제 1.8.4.
Q. 집합 $A = \{1,\, 2,\, \ldots,\, 2n-1\}$에서 원소의 개수가 $n+1$인 부분집합 $B$를 임의로 택할 때, 합이 $2n$이 되는 $B$의 원소 두 개를 언제나 택할 수 있음을 보여라.
A. 다음과 같은 $n$개의 $A$의 부분집합들을 생각하자. \[ \{1,\, 2n-1\},\, \{2,\, 2n-2\},\, \ldots,\, \{n-1,\, n+1\},\, \{n\}. \] 위에서 집합 $\{n\}$를 제외한 부분집합의 원소의 합은 언제나 $2n$이 된다. 한편, 비둘기집의 원리에 의해 원소의 개수가 $n+1$인 부분집합 $B$는 위 $n$개의 집합 중 $\{n\}$를 제외한 나머지 하나를 부분집합으로 가져야 한다. 따라서 그 부분집합에 속한 두 원소의 합은 $2n$이 된다. $ $

$ $

예제 1.8.5.
Q. 숫자 $1$로만 이루어진 수의 열 \[ 1,\, 11,\, 111,\, 1111 \ldots \] 중에는 $7$의 배수가 반드시 존재함을 증명하여라.
A. 위의 수열을 $333$로 나눈 나머지는 $0,\, 1,\, 2,\, \ldots,\, 332$의 $333$가지 중 하나이다. 따라서 비둘기집의 원리에 의해 위 수열의 각 항을 $333$으로 나누었을 때 나머지가 같은 두 수가 반드시 존재한다. 이 두 수의 차는 $333$의 배수이면서 \[ n = 11 \cdots 1 00 \cdots 0 \] 의 형태를 갖는다. 한편 $333$은 $10$과 서로소이므로 $n$에서 $0$을 모두 지운 $11 \cdots 1$ 또한 $333$의 배수가 된다. $ $

$ $

예제 1.8.6.
Q. $a_1,\, a_2,\, \ldots,\, a_n$이 양의 정수열이라 하자. 그러면 다음 연속적인 부분 정수열의 합 \[ a_{i+1} + a_{i+2} + \cdots + a_{j} \] 이 $n$의 배수가 되도록 하는 $i < j$가 반드시 존재함을 보여라.
A. 다음 $n$개의 합을 생각하자. \begin{align*} s_1 & = a_1, \\[1ex] s_2 & = a_1 + a_2, \\[1ex] s_3 & = a_1 + a_2 + a_3, \\ & \;\; \vdots \\ s_n & = a_1 + a_2 + \cdots + a_n. \end{align*} 위 합들은 모두 연속적인 부분 정수열의 합이므로, 이 중에 $n$의 배수가 있다면 증명이 끝이 난다.

이제 모든 합 $s_1,\, \ldots,\, s_n$이 $n$의 배수가 아니라고 가정해 보자. 이 경우 각각의 합을 $n$으로 나누었을 때의 나머지는 $\{1,\, 2,\, \ldots,\, n-1\}$ 중에 하나이므로, 비둘기집의 원리에 의해 나머지가 같은 두 집합 $s_i$, $s_j$가 반드시 존재한다. 편의상 $i < j$라 하면 \[ s_j - s_i = a_{i+1} + a_{i+2} + \cdots + a_{j} \] 는 $n$으로 나누어 떨어지는 연속적인 부분 정수열의 합이 된다. $ $

$ $

예제 1.8.7.
Q. 어떤 학생이 $10$일동안 총 $15$시간의 이산수학 공부를 하였다. 이 학생은 매일 적어도 $1$시간씩 공부를 했다고 하면, 이 학생이 며칠동안 공부한 시간의 총합이 정확히 $4$시간이 되는 경우가 있음을 보여라. (단, 이 학생은 매일 정확히 $1$시간 단위로만 공부를 한다.)
A. $i = 1,\, \ldots,\, 10$에 대하여 $a_i$를 이 학생이 첫날부터 $i$번째 날까지 공부한 시간의 총합으로 정의하자. 그러면 다음 부등식 \[ 1 \leq a_1 < a_2 < \cdots < a_{10} = 15 \] 가 성립해야 한다. 이제 다음 $20$개의 양의 정수 \[ a_1,\, a_2,\, \ldots,\, a_{10},\, a_{1} + 4 ,\, a_{2} + 4,\, \ldots,\, a_{10} + 4 \] 를 생각해 보자. 그러면 비둘기집의 원리에 의해 적어도 두 양의 정수는 같은 값을 가져야 한다. 하지만 $a_1,\, a_2,\, \ldots,\, a_{10}$는 모두 다른 수들이고, 마찬가지로 $a_{1} + 4 ,\, a_{2} + 4,\, \ldots,\, a_{10} + 4$ 또한 모두 다른 수들이기 때문에, 적당한 $i,\, j$에 대하여 $a_i = a_{j} + 4$가 성립해야 한다. 이를 정리하면 \[ a_i - a_j = 4 \] 이고, 즉, $j+1$번째 날부터 $i$번쨰 날까지 공부한 시간의 총합이 정확히 $4$시간이 된다. $ $

$ $

예제 1.8.8.
Q. $n$명이 참가한 어느 모임에서 참가자들은 다른 참가자들과 악수를 하였다. 이 모임에 참가한 사람 중에는 악수한 횟수가 같은 두 사람이 존재함을 보여라.
A. $n$명의 사람들을 $A_1,\, A_2,\, \ldots,\, A_n$으로 나타내고 이 사람들이 악수한 횟수를 $k_1,\, k_2,\, \ldots,\, k_n$으로 나타내자. 그러면 각 참가자는 자기 자신과 악수를 할 수 없으므로 모든 $i = 1,\, 2,\, \ldots,\, n$에 대하여 $0 \leq k_i \leq n-1$이 성립한다. 이제 다음 두 가지 경우를 나누어 생각해 보자.

• 모든 사람들이 적어도 한 번씩은 악수를 한 경우: 이때는 각각의 $i = 1,\, 2,\, \ldots,\, n$에 대하여 $1 \leq k_i \leq n-1$이 성립한다. 따라서 비둘기집의 정리에 의해 $k_1,\, k_2,\, \ldots,\, k_n$ 중 적어도 같은 두 수가 존재한다.
• 한 번도 악수를 하지 않은 사람이 존재하는 경우: 편의상 이 사람을 $A_1$이라 하자. 그러면 모든 $i \neq 1$에 대하여 $A_i$는 $A_1$과는 악수를 하지 않았으므로, $k_i$는 $n-1$이 될 수 없다. 따라서 모든 $i$에 대하여 $0 \leq k_i \leq n-2$임을 알 수 있다. 그러므로 이 경우에도 비둘기집의 정리에 의해 $k_1,\, k_2,\, \ldots,\, k_n$ 중 적어도 같은 두 수가 존재한다. $ $

$ $

예제 1.8.9.
Q. $1$ 부터 $100$ 까지의 양의 정수들을 다음 조건을 모두 만족하는 두 집합 $\{a_{1},\, \ldots,\, a_{50}\}$과 $\{b_{1},\, \ldots,\, b_{50}\}$으로 분할한다. \[ a_{1} < a_{2} < \cdots < a_{50}, \quad b_{1} > b_{2} > \cdots > b_{50}. \] 이제 이 분할에 대하여, $S$를 다음과 같이 정의한다. \[ S = \abs{a_{1} - b_{1}} + \abs{a_{2} - b_{2}} + \cdots + \abs{a_{50} - b_{50}} \] 이 때, 위 조건을 만족하는 임의의 분할에 대하여, $S$가 가질 수 있는 값을 모두 구하여라.
A. 먼저 모든 $1 \leq n \leq 50$에 대하여, \begin{align*} & 1 \leq \min\{a_{n},\, b_{n}\} \leq 50 \tag*{$\myblue{(1)}$} \\[1ex] & 51 \leq \max\{a_{n},\, b_{n}\} \leq 100 \tag*{$\myblue{(2)}$} \end{align*} 을 동시에 만족함을 보일 것이다.
만약 위 명제가 성립하지 않는다 가정하자. 그러면 적당한 $1 \leq k \leq 50$가 존재하여, ($\myblue{(1)}$을 만족하지 않는 경우) $a_{k},\, b_{k} \geq 51$이거나 ($\myblue{(2)}$를 만족하지 않는 경우) $a_{k},\, b_{k} \leq 50$이 성립한다. 하지만 만약 $a_{k},\, b_{k} \geq 51$인 경우 \begin{align*} 51 \leq a_{k} < a_{k+1} < \cdots < a_{50} \leq 100 \\[1ex] 51 \leq b_{k} < b_{k-1} < \cdots < b_{1} \leq 100 \end{align*} 가 되어 총 $51$개의 서로 다른 양의 정수 \[ b_1,\, b_2,\, \ldots,\, b_{k},\, a_{k},\, a_{k+1},\, \ldots,\, a_{50} \] 이 $51$과 $100$ 사이에 존재해야 하는데, 이는 비둘기집의 원리에 의해 불가능하다. 또한 $a_{k},\, b_{k} \leq 50$인 경우에도 비슷한 논리로 모순을 이끌어 낼 수 있다. 따라서 모든 $1 \leq n \leq 50$에 대하여 식 $\myblue{(1)}$과 $\myblue{(2)}$가 동시에 성립한다.
한편, 임의의 실수 $a,\,b$에 대하여 \[ \abs{a-b} = \max\{a,\,b\} - \min\{a,\,b\} \] 가 성립하므로, \begin{align*} S & = \sum_{n=1}^{50} \abs{a_{n} - b_{n}} \\[1ex] & = \sum_{n=1}^{50} \big( \max\{a_{n},\, b_{n}\} - \min\{a_{n},\, b_{n}\} \big) \\[1ex] & = \sum_{n=1}^{50} \max\{a_{n},\, b_{n}\} - \sum_{n=1}^{50} \min\{a_{n},\, b_{n}\} \\[1ex] & = (51 + 52 + \cdots + 100) - (1 + 2 + \cdots + 50) \\[1ex] & = 2500 \end{align*} 을 얻는다. 따라서 주어진 조건을 만족하는 임의의 분할에 대하여 $S$의 값은 언제나 $2500$임을 알 수 있다. $ $

$ $

비둘기집의 원리를 일반화 하면 다음과 같은 정리를 얻을 수 있다.

$ $

정리 1.8.10. 일반화된 비둘기집의 원리_{(generalized pigeonhole principle)}

두 집합 $X,\, Y$에 대하여 $\abs{X} = n$, $\abs{Y} = m$이라 가정하자. 그러면 임의의 함수 $f : X \to Y$에 대하여, $\abs{f^{-1}(\{y\})} \geq \big\lceil \frac{n}{m} \big\rceil$를 만족하는 $y \in Y$가 적어도 하나 존재한다.

$ $

증명. 결론에 반하여, 모든 $y \in Y$에 대하여 \[ \abs{f^{-1}(\{y\})} < \Big\lceil \dfrac{n}{m} \Big\rceil \] 라 가정해보자. 그러면 \[ \abs{f^{-1}(\{y\})} \leq \Big\lceil \dfrac{n}{m} \Big\rceil - 1 \] 이 성립하므로 \begin{align*} n = \sum_{y \in Y} \abs{f^{-1}(\{y\})} & \leq m \Big( \Big\lceil \frac{n}{m} \Big\rceil - 1 \Big) \\[1ex] & < m \Big( \! \Big( \frac{n}{m} + 1 \Big) - 1 \Big) \\[1ex] & = n \end{align*} 이 되어 모순이다. 따라서 $\abs{f^{-1}(\{y\})} \geq \big\lceil \frac{n}{m} \big\rceil$를 만족하는 $y \in Y$가 적어도 하나 존재한다. $ $

$ $

예제 1.8.11.
Q. 한 편의 길이가 $3$인 정사각형의 내부에 어떤 세 점도 한 직선 위에 있지 않도록 $19$개의 점을 임의의 잡으면 그 중에는 넓이가 $\dfrac{1}{2}$ 이하인 삼각형의 꼭짓점을 이루는 세 점이 반드시 존재함을 보여라.
A. 다음과 같이 주어진 정사각형을 한 편의 길이가 $1$인 $9$개의 작은 정사각형으로 나누어 보자.

$ $

$ $

그러면 일반화된 비둘기집의 원리에 의해 점을 $\big\lceil \frac{19}{9} \big\rceil = 3$개 이상 포함하는 정사각형이 반드시 존재하고 이 정사각형 안에 있는 세 점으로 이루어지는 삼각형의 넓이는 $\dfrac{1}{2}$ 이하여야만 한다. $ $

$ $

예제 1.8.12.
Q. 학생들의 이산수학 성적을 $A,\, B,\, C,\, D,\, F$로 매길 때, $4$명의 같은 성적을 받은 학생이 존재하기 위해서는 적어도 몇 명의 학생이 이산수학 수업을 들어야 하는지 구하여라.
A. 이산수업 수업을 듣는 학생 수를 $n$명이라 하자. 그러면 일반화된 비둘기집의 원리에 의해 적어도 $\big\lceil \frac{n}{5} \big\rceil$명의 학생들이 같은 성적을 받아야 한다. 따라서 \[ \Big\lceil \frac{n}{5} \Big\rceil = 4 \implies 3 < \frac{n}{5} \leq 4 \implies 15 < n \leq 20 \] 따라서 적어도 $16$명의 학생이 이산수학 수업을 들어야 한다. $ $

$ $

비둘기집의 원리를 이용한 다음 예제를 살펴보자.

$ $

예제 1.8.13.
Q. $6$명의 사람이 있다고 하자. 이 사람들 중 어떤 두 사람은 서로 알거나, 혹은 서로 모르는 사이이다. 그러면 이 $6$명의 사람 중에서 서로 아는 사이인 $3$명의 사람, 또는 서로 모르는 사이인 $3$명의 사람이 반드시 존재함을 증명하여라.
A. $6$명의 사람들을 점으로 표현하고, 어떤 두 사람이 서로 알고 있다면 해당되는 두 점을 파란색 변으로, 그렇지 않다면 해당되는 두 점을 검은색 변으로 연결해보자. 그러면 예를 들어 아래와 같은 그래프를 얻는다.

$ $

$ $

그러면 위 문제는 변의 색이 모두 파란색이거나 모두 검은색인 삼각형이 반드시 존재함을 보이는 문제와 같다.
이제 위 그래프의 한 점 $A_1$과 연결된 $5$개의 변을 생각하면, 일반화된 비둘기집의 원리에 의해 적어도 $\big\lceil \frac{5}{2} \big\rceil = 3$개의 변은 같은 색 $C$를 가져야 한다. 나머지 다른 색을 편의상 $D$라 하자. 이제 이 $3$개의 변들과 연결된 반대쪽 점들을 생각해 보자. 만약 이 세 점을 연결하는 변 중 색 $C$를 갖는 변이 존재한다면 그 변의 양 끝 점과 $A_1$이 모두 같은 색 $C$를 갖는다. 반대로 이 세 점을 연결하는 변이 모두 색 $C$를 갖지 않는다면 이 세 점을 연결하는 삼각형은 모두 같은 색 $D$를 갖는다. $ $

$ $

참고. 양의 정수 $n$에 대하여 $K_n$이란 $n$개의 점과 서로 다른 두 점이 모두 변으로 연결된 완전그래프_{(complete graph)}를 나타낸다. 이제 각각의 변을 $C$ 또는 $D$의 색으로 칠했다고 했을 때, $R(i,\, j)$는 모든 변의 색이 $C$인 완전그래프 $K_i$, 또는 모든 변의 색이 $D$인 완전그래프 $K_j$가 반드시 존재하게 되는 최소의 완전그래프 $K_n$에서의 $n$을 나타내며, 이를 램지 수_{(Ramsey number)}라 한다. $ $

$ $

임의의 양의 정수 $i,\, j$에 대하여 $R(i,\, j) = R(j,\, i)$이 성립하고, 나아가 모든 양의 정수 $i$에 대하여 $R(i,\, 1) = 1$이 성립한다. 그리고 앞서 살펴본 예제 1.8.13을 이용하면 $R(3,\, 3)$에 대한 값을 구할 수 있다.

$ $

정리 1.8.14.

$R(3,\, 3) = 6$.

$ $

증명. 위 예제 1.8.13에 의해서 $R(3,\, 3) \leq 6$을 얻는다. 완전그래프 $K_5$의 각각의 변을 다음과 같이 칠하면

$ $

$ $

변의 색이 모두 파란색이거나 모두 검은색인 완전그래프 $K_3$가 존재하지 않으므로 $R(3,\, 3) > 5$가 되어, $R(3,\, 3) = 6$이라는 결론을 얻는다. $ $

$ $

정리 1.8.15.

$i \geq 2$에 대하여 $R(i,\, 2) = i$.

$ $

증명. 우선 $R(i,\, 2) \geq i$임은 자명하다. 이제 완전그래프 $K_i$의 모든 변을 $C$ 또는 $D$의 색으로 칠했다고 가정하자. 만약 모든 변의 색이 $C$라면 증명이 완료되고, 어떤 변의 색이 $D$라 하면 모든 변의 색이 $D$인 $K_2$가 존재하는 것이므로 마찬가지로 증명이 끝이 난다. $ $

$ $

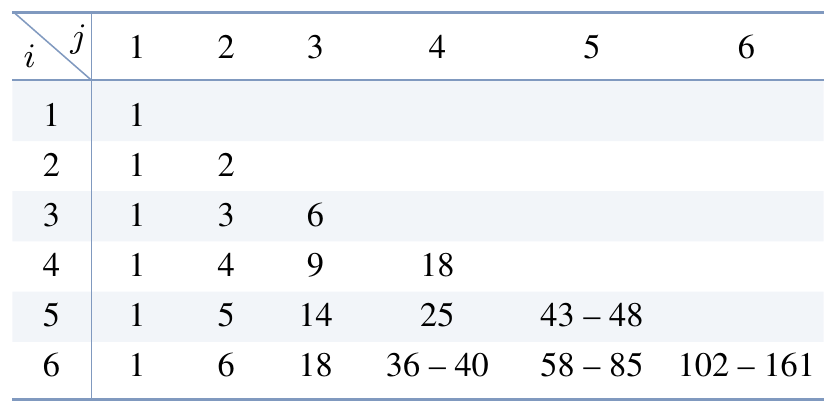
위와 같이 간단한 경우를 제외한 대부분의 경우, 램지 수에 대한 정확한 값은 알려져 있지 않고 범위의 형태로만 확인되어 있다. $i,\, j \leq 6$에 대하여 현재까지 알려진 램지 수는 다음과 같다.

$ $

$ $

위와 같이 수학적 구조의 크기에 따라 나타나는 특정한 질서를 연구하는 분야를 램지 이론_{(Ramsey theory)}이라 한다.

$ $

정리 1.8.16. 램지 수에 대한 상한

임의의 양의 정수 $i \geq j \geq 2$에 대하여 \[ R(i,\, j) \leq R(i-1,\, j) + R(i,\, j-1). \]

$ $

증명. 점의 개수가 $R(i-1,\, j) + R(i,\, j-1)$인 완전그래프의 각각의 변을 $C$ 또는 $D$의 색으로 칠했다고 가정하자. 우리는 이 그래프에서 모든 변의 색이 $C$인 부분 완전그래프 $K_{i}$가 존재하거나 모든 변의 색이 $D$인 부분 완전그래프 $K_{j}$가 존재함을 보여야 한다. 이제 이 그래프의 한 점 $v$와 색 $C$로 칠해진 변으로 연결된 점들의 집합을 $V_{C}$, 색 $D$로 칠해진 변으로 연결된 점들의 집합을 $V_{D}$로 정의하자. 그러면 \[ \abs{V_{C}} + \abs{V_{D}} = R(i-1,\, j) + R(i,\, j-1) - 1 \] 이 성립한다.
만약 $\abs{V_{C}} < R(i-1,\, j)$와 $\abs{V_{D}} < R(i,\, j-1)$이 동시에 성립하면, $\abs{V_{C}} + 1 \leq R(i-1,\, j)$와 $\abs{V_{D}} +1 \leq R(i,\, j-1)$이 동시에 성립하므로 \begin{align*} \abs{V_{C}} + \abs{V_{D}} & = R(i-1,\, j) + R(i,\, j-1) - 1 \\[1ex] & \geq (\abs{V_{C}} + 1) + (\abs{V_{D}} + 1) - 1 \\[1ex] & = \abs{V_{C}} + \abs{V_{D}} + 1 \end{align*} 이 되어 모순이 발생한다. 따라서 $\abs{V_{C}} \geq R(i-1,\, j)$ 또는 $\abs{V_{D}} \geq R(i,\, j-1)$이 성립해야만 한다. 이제 두 가지 경우를 나누어 생각해 보자.

• $\abs{V_{C}} \geq R(i-1,\, j)$인 경우: 완전그래프 $K_{\abs{V_{C}}}$는 모든 변의 색이 $C$인 부분 완전그래프 $K_{i-1}$을 갖거나, 모든 변의 색이 $D$인 부분 완전그래프 $K_j$를 가져야 한다. 하지만 처음 경우에도 $K_{i-1}$에 점 $v$를 추가한 완전그래프의 모든 변의 색이 $C$가 된다.
• $\abs{V_{D}} \geq R(i,\, j-1)$인 경우: 위와 마찬가지로 완전그래프 $K_{\abs{V_{C}}}$는 모든 변의 색이 $C$인 부분 완전그래프 $K_{i}$를 갖거나, 모든 변의 색이 $D$인 부분 완전그래프 $K_{j-1}$을 가져야 한다. 하지만 두번째 경우에도 $K_{j-1}$에 점 $v$를 추가한 완전그래프의 모든 변의 색은 $D$가 된다.

어떠한 경우에도 모든 변의 색이 $C$인 부분 완전그래프 $K_{i}$가 존재하거나 모든 변의 색이 $D$인 부분 완전그래프 $K_{j}$가 존재하므로 주어진 부등식이 성립한다. $ $

$ $

참고. 정리 1.8.16을 이용하면 임의의 양의 정수 $i \geq j \geq 1$에 대하여 \[ R(i,\, j) \leq \binom{i+j-2}{i-1} \] 임을 증명할 수 있다. 먼저 $i = j = 1$인 경우, \[ R(i,\, j) = R(1,\, 1) = 1 = \binom{1}{0} = \binom{i+j-2}{i-1} \] 이라 할 수 있고, 이항계수에 대한 성질에 의해 \begin{align*} R(i,\, j) & = R(i-1,\, j) + R(i,\, j-1) \\[1ex] & \leq \binom{i+j-3}{i-2} + \binom{i+j-3}{i-1} \\[1ex] & = \binom{i+j-2}{i-1} \end{align*} 가 성립하므로 수학적 귀납법에 의해 증명이 완료된다. $ $

$ $