예제 1.6.1.
Q. 집합 $A = \{1,\, 2,\, 3,\, 4\}$를 공집합이 아니고 쌍마다 서로소인 부분집합들의 합집합으로 나타내는 방법의 수는 몇 가지인가?
A. 직접 구해보면 \[ \begin{array}{llllll} \{1,\, 2,\, 3,\, 4\} & \phantom{xxx} & \{1\} \cup \{2\} \cup \{3\} \cup \{4\} & & & \\ \{1\} \cup \{2,\, 3,\, 4\} & \phantom{x} & \{2\} \cup \{1,\, 3,\, 4\} & & & \\ \{3\} \cup \{1,\, 2,\, 4\} & \phantom{x} & \{4\} \cup \{1,\, 2,\, 3\} & & & \\ \{1,\, 2\} \cup \{3,\, 4\} & \phantom{x} & \{1\} \cup \{2\} \cup \{3,\, 4\} & \phantom{x} & \{1,\, 2\} \cup \{3\} \cup \{4\} & \\ \{1,\, 3\} \cup \{2,\, 4\} & \phantom{x} & \{1\} \cup \{3\} \cup \{2,\, 4\} & \phantom{x} & \{1,\, 3\} \cup \{2\} \cup \{4\} & \\ \{1,\, 4\} \cup \{2,\, 3\} & \phantom{x} & \{1\} \cup \{4\} \cup \{2,\, 3\} & \phantom{x} & \{1,\, 4\} \cup \{2\} \cup \{3\} & \end{array} \] 이 되어 모두 15가지임을 알 수 있다. $ $

$ $

정의 1.6.2. 집합의 분할_{(set partition)}

$\abs{A} = n$인 집합 $A$의 부분집합 $B_1,\, B_2,\, \ldots,\, B_k$가 다음 조건

1. 모든 $i$에 대하여 $B_i \neq \emptyset$
2. $A = B_1 \cup B_2 \cup \cdots \cup B_k$
3. 모든 $i \neq j$에 대하여 $B_i \cap B_j = \emptyset$

을 모두 만족할 때, $\pi = (B_1,\, B_2,\, \ldots,\, B_k)$를 집합 $A$의 분할_{(set partition)}이라 한다.

$ $

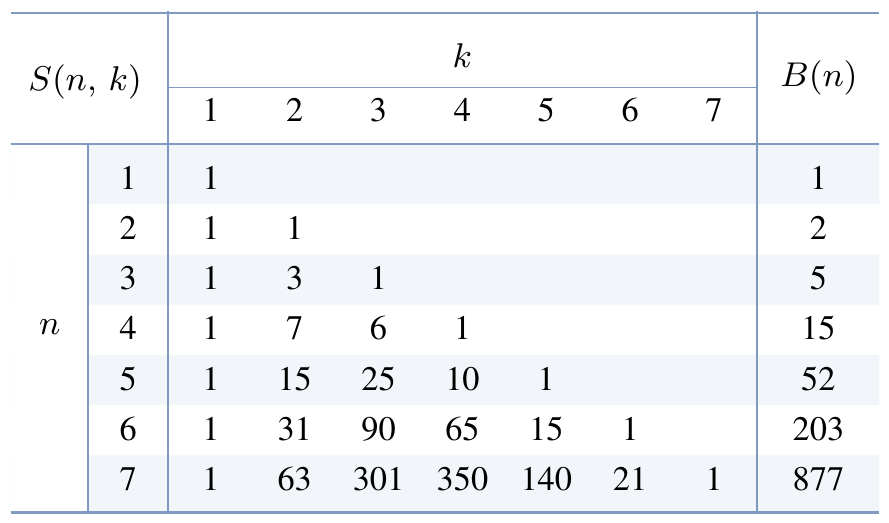
$\abs{A} = n$인 집합 $A$의 모든 분할의 개수를 벨 수_{(Bell number)}라 부르고 기호로는 $B(n)$으로 나타낸다. 또한 $k$개의 부분집합을 가지는 $A$의 분할의 개수를 제2종 스털링 수_{(Stirling number of the second kind)}라 부르고 기호로는 $S(n,\, k)$으로 나타낸다. 따라서 정의에 의해 \begin{align*} B(n) & = \sum_{k=1}^{n} S(n,\, k) \\[1ex] & = S(n,\, 1) + S(n,\, 2) + \cdots + B(n,\, n) \end{align*} 이 성립한다. 위의 예제 1.6.1에서 \[ B(4) = 15, \quad S(4,\, 2) = 7, \quad S(4,\, 3) = 6 \] 과 같은 식이다.

$ $

$n = 1,\, 2,\, 3,\, \ldots$일 때, $B(n)$의 값을 계산해 보면 \[ 1,\, 2,\, 5,\, 15,\, 52,\, 203,\, 877,\, 4140,\, \ldots \]

$ $

정리 1.6.3. 제2종 스털링 수에 대한 점화식

$n \geq k$인 양의 정수 $n,\, k$에 대하여 \[ S(n,\, k) = S(n-1,\, k-1) + k S(n-1,\, k). \]

$ $

증명. 집합 $A = \{1,\, 2,\, \ldots,\, n\}$, $B = A \setminus \{1\}$이라 하고 $A$를 $k$개의 부분집합으로 나누는 분할을 다음 두 가지 경우로 나누어 생각하자.

• 원소 $1$이 홀로 한 부분집합을 이루는 경우: 이 경우, $B$를 $k-1$개의 부분집합으로 분할하면 충분하므로 모든 경우의 수는 \[ S(n-1,\, k-1) \]
• 원소 $1$이 다른 부분집합의 원소가 되는 경우: 이는 $B$를 $k$개의 부분집합으로 분할하고, $k$개의 부분집합 중 하나에 원소 $1$을 포함시키는 경우의 수와 같으므로 \[ k S(n-1,\, k) \]

위 두 경우는 동시에 일어나지 않으므로, \[ S(n,\, k) = S(n-1,\, k-1) + k S(n-1,\, k) \] 를 얻는다. $ $

$ $

위 정리를 이용하여 $B(n)$의 값을 구해보면

$ $

$ $

다음 정리는 벨 수에 대한 점화식을 나타낸다.

$ $

정의 1.6.4. 벨 수에 대한 점화식

양의 정수 $n$에 대하여 \[ B(n+1) = \sum_{k=0}^{n} \binom{n}{k} B(k). \] 단, $B(0) = 1$로 정의한다.

$ $

증명. 집합 $A = \{1,\, 2,\, \ldots,\, n+1\}$의 분할 중에서 원소 $1$을 포함하는 부분집합 $A_1$의 원소의 개수가 정확히 $k$가 되도록 하는 분할의 개수를 구해보자. 이는 $1$을 제외한 $n$개의 원소 중에서 $A_1$의 원소가 될 $k-1$개의 원소를 선택하고, 나머지 $n+1-k$의 원소를 임의로 분할하는 경우의 수와 같으므로 \[ \binom{n}{k-1} B(n+1-k) \] 를 얻는다. 이 때, $k$가 택할 수 있는 값은 $k = 1,\, 2,\, \ldots,\, n+1$이 가능하므로 \begin{align*} B(n+1) & = \sum_{k=1}^{n+1} \binom{n}{k-1} B(n+1-k) \\[1ex] & = \sum_{k=0}^{n} \binom{n}{k} B(n-k) \\[1ex] & = \sum_{k=0}^{n} \binom{n}{n-k} B(n-k) \\[1ex] & = \sum_{k=0}^{n} \binom{n}{k} B(k). \tag*{$\myblue{\blacksquare}$} \end{align*}

$ $

예제 1.6.5.
Q. $5$개의 서로 다른 종류의 공과 $3$개의 같은 종류의 상자가 있다고 하자. 이때, 다음 경우의 수를 각각 구하여라.

1. 빈 상자가 없도록 상자에 공을 넣는 방법의 수
2. 상자에 공을 넣는 방법의 수

A.

1. 전체 방법의 수는 원소의 개수가 $5$개인 집합을 쌍마다 서로소인 $3$개의 부분집합으로 분할하는 경우의 수와 같다. 따라서 \[ S(5,\, 3) = 25. \]
2. 빈 상자가 있을 수도 있으므로 전체 방법의 수는 원소의 개수가 $5$개인 집합을 쌍마다 서로소인 $3$개 이하의 부분집합으로 분할하는 경우의 수와 같다. 따라서 \[ p(5,\, 1) + p(5,\, 2) + p(5,\, 3) = 1 + 15 + 25 = 41. \tag*{$\myblue{\blacksquare}$} \]

$ $

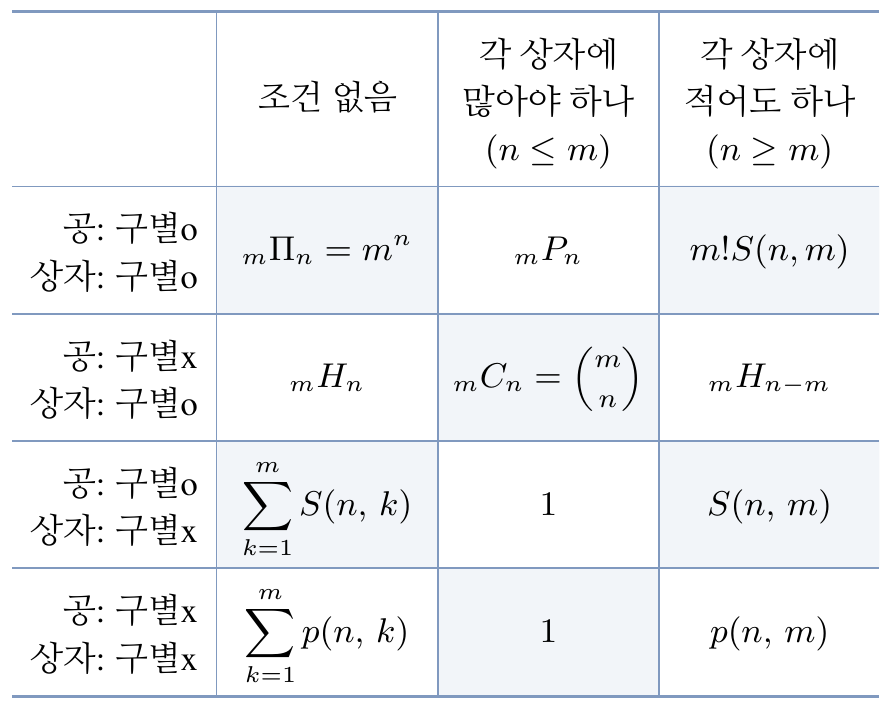
지금까지 $n$개의 공을 $m$개의 상자에 담은 경우의 수에 관한 문제를 여러가지 살펴보았다. 각각의 공과 상자가 서로 구별 가능 여부에 따라 다양한 경우의 수가 나오게 되는데 이를 정리한 것이 아래에 설명할 12갈래 방법_{(twelvefold way)}이다.

$ $

$ $

특히, 위 표에서 첫번째 행의 수들은 두 집합 $X,\, Y$의 크기가 각각 $\abs{X} = n$, $\abs{Y} = m$으로 주어졌을 때, $X$에서 $Y$로 가는 모든 함수, 단사_(injective) 함수, 전사_(surjective) 함수의 개수와 같다.

$ $

예제 1.6.6.
Q. 두 집합 $X,\, Y$의 크기가 각각 $\abs{X} = n$, $\abs{Y} = m$으로 주어졌을 때, 치역의 크기가 $k$인 $X$에서 $Y$로 가는 함수의 개수를 구하여라.
A. 위 조건을 만족하는 함수는 먼저 크기가 $k$인 공역 $Y$의 부분집합 $Z$를 선택한 뒤 $X$에서 $Z$로 가는 전사함수와 같다. 부분집합 $Z$를 택하는 경우의 수는 $\binom{m}{k}$이고 $X$에서 $Z$로 가는 전사함수의 개수는 $k!S(n, k)$이므로 곱의 법칙에 의해 \[ \binom{m}{k} k! S(n,\, k). \tag*{$\myblue{\blacksquare}$} \]

$ $

참고. 두 집합 $X,\, Y$의 크기가 각각 $\abs{X} = n$, $\abs{Y} = m$으로 주어졌을 때 $X$에서 $Y$로 가는 모든 함수의 개수는 $m^n$임을 확인하였다. 또한 이는 $k = 1,\, \ldots,\, m$에 대하여 치역의 크기가 $k$인 함수들의 개수의 합과 같다. 그러므로 \[ m^n = \sum_{k=1}^{m} \binom{m}{k} k! S(n,\, k) \] 이 성립한다. 이를 이용하면 다음과 같이 $n$제곱 수들의 합에 대한 공식을 얻을 수 있다. \begin{align*} \sum_{p=1}^{m} p^n & = \sum_{p=1}^{m} \sum_{k=1}^{p} \binom{p}{k} k! S(n,\, k) \\[1ex] & = \sum_{k=1}^{m} \sum_{p=k}^{m} \binom{p}{k} k! S(n,\, k) \\[1ex] & = \sum_{k=1}^{m} k! S(n,\, k) \bigg( \sum_{p=k}^{m} \binom{p}{k} \bigg) \\[1ex] & = \sum_{k=1}^{m} k! S(n,\, k) \binom{m+1}{k+1}. \tag*{$\myblue{\square}$} \end{align*}

$ $