행렬 $A \in \mathbb{R}^{n \times n}$의 대각 성분 아래 성분만으로 이루어진 하삼각행렬을 $L$, 대각성분만으로 이루어진 대각행렬을 $D$, 그리고 대각성분 위에 있는 성분만으로 이루어진 상삼각행렬을 $U$라 하면 \[ A = L + D + U \] 와 같이 두었을 때, $N = D+L$, $P = -U$로 정의하여 반복법을 수행하는 것을 가우스-자이델 방법(Gauss-Seidel method)이라 한다. 가우스-자이델 방법을 적용하면 \[ (D+L) \mathbf{x}^{(k)} = \mathbf{b} -U\mathbf{x}^{(k-1)} \] 또는 위 식을 정리하여 \[ \mathbf{x}^{(k)} = D^{-1} \big[ \mathbf{b} - L \mathbf{x}^{(k)} - U \mathbf{x}^{(k-1)} \big] \] 을 얻고, 위 식에서 벡터 $\mathbf{x}^{(k)}$의 $i$번째 성분은 \[ x^{(k)}_i = \frac{1}{a_{ii}} \Bigg[ b_i - \sum_{j=1}^{i-1} a_{ij}x^{(k)}_j - \sum_{j=i+1}^{n} a_{ij} x^{(k-1)}_j \Bigg] \] 로 주어진다. 가우스-자이델 방법에서는 $\Norm{(D+L)^{-1}U} < 1$이 성립하면 임의의 초기벡터 $\mathbf{x}^{(0)}$에 대한 벡터열 $(\mathbf{x}^{(k)})$가 실제 선형연립방정식의 해로 수렴한다.
$ $
참고. 야코비 방법과 가우스-자이델 방법에서 새로운 벡터 $x^{(k)}$의 $i$번째 성분 $x^{(k)}_i$를 계산하는 과정을 비교해보자.
- 야코비 방법에서는 이전 벡터 $x^{(k-1)}$의 성분 $x^{(k-1)}_j$, $j = 1,\, \ldots,\, i-1,\, i+1,\, \ldots,\, n$만을 사용한다.
- 가우스-자이델 방법에서는 이전 벡터 $x^{(k-1)}$의 성분 $x^{(k-1)}_j$, $j = i+1,\, \ldots,\, n$ 뿐만 아니라 새로운 벡터의 성분 $x^{(k)}_j$, $로j = 1,\, \ldots,\, i-1$ 또한 사용하게 된다.
새로운 벡터의 성분 $x^{(k)}_j$들이 이전 벡터의 성분 $x^{(k-1)}_j$들 보다 개선된 것이므로, 해가 수렴한다고 가정하면 가우스-자이델 방법의 수렴 속도가 대체적으로 야코비 방법의 수렴 속도보다 빠르다고 할 수 있다.$ $
$ $
예제 1.6.1.
Q. 선형연립방정식의 첨가행렬이 다음과 같이 주어졌다고 하자.
\[ [ A \,|\, \mathbf{b} ] = \left[ \, \begin{array}{rrr|r}
4 & 1 & -1 & 4 \\
1 & -4 & 2 & -1 \\
0 & -3 & 4 & 1
\end{array} \, \right] \]
이 때, 초기값을 $\mathbf{x}^{(0)} = (0,\, 0,\, 0)$으로 하고 가우스-자이델 방법을 이용하여 해를 구하여라.
A. 가우스-자이델 방법을 이용하여 $\mathbf{x}^{(1)},\, \mathbf{x}^{(2)}$를 구해보자.
\begin{align*}
\mathbf{x}^{(1)} & = (D+L)^{-1} \big( \mathbf{b} -U\mathbf{x}^{(0)} \big) \\[1ex]
& = \begin{bmatrix}
\frac{1}{4} & 0 & 0 \\
\frac{1}{16} & -\frac{1}{4} & 0 \\
\frac{3}{64} & -\frac{3}{16} & \frac{1}{4}
\end{bmatrix} \left( \begin{bmatrix} 4 \\ -1 \\ 1 \end{bmatrix} - \begin{bmatrix}
0 & 1 & -1 \\
0 & 0 & 2 \\
0 & 0 & 0
\end{bmatrix} \begin{bmatrix} 0 \\ 0 \\ 0 \end{bmatrix} \right) \\[1ex]
& = \begin{bmatrix} 1 \\ \frac{1}{2} \\ \frac{5}{8} \end{bmatrix} \\[2ex]
\mathbf{x}^{(2)} & = (D+L)^{-1} \big( \mathbf{b} -U\mathbf{x}^{(1)} \big) \\[1ex]
& = \begin{bmatrix}
\frac{1}{4} & 0 & 0 \\
\frac{1}{16} & -\frac{1}{4} & 0 \\
\frac{3}{64} & -\frac{3}{16} & \frac{1}{4}
\end{bmatrix} \left( \begin{bmatrix} 4 \\ -1 \\ 1 \end{bmatrix} - \begin{bmatrix}
0 & 1 & -1 \\
0 & 0 & 2 \\
0 & 0 & 0 \end{bmatrix} \begin{bmatrix} 1 \\ \frac{1}{2} \\ \frac{5}{8} \end{bmatrix} \right) \\[1ex]
& = \begin{bmatrix} \frac{33}{32} \\[1ex] \frac{105}{128} \\[1ex] \frac{443}{512} \end{bmatrix} \eqqed
\end{align*}
$ $
참고. 실제로 MATLAB을 이용하여 $\norm{\mathbf{x}^{(k)} - \mathbf{x}^{(k-1)}} < 0.00001$을 만족할 때까지 가우스-자이델 방법을 반복하면,
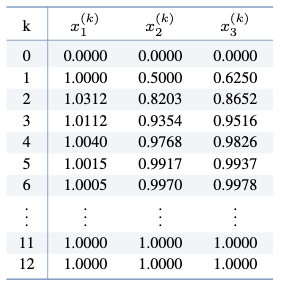가 되어 총 $k=12$번의 가우스-자이델 방법의 반복 계산을 통해 $\mathbf{x} = (1,\, 1,\, 1)$이 해가됨을 알 수 있다.$ $
$ $
벡터 $\mathbf{x}^{(k-1)}$로부터 새로운 벡터 $\mathbf{x}^{(k)}$를 찾는 과정을 생각해 보자. \[ \mathbf{x}^{(k)} = \mathbf{x}^{(k-1)} + (\mathbf{x}^{(k)} - \mathbf{x}^{(k-1)}) \] 로 나타낼 수 있으므로, $\mathbf{x}^{(k)}$는 $\mathbf{x}^{(k-1)}$로부터 $\mathbf{x}^{(k)} - \mathbf{x}^{(k-1)}$ 방향으로 이동한 것이라 볼 수 있다.
$ $
$ $
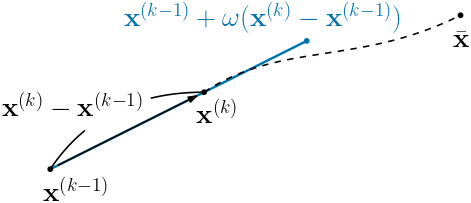
이 벡터열이 선형연립방정식의 해 $\bar{\mathbf{x}}$로 수렴한다고 가정하면, $\mathbf{x}^{(k-1)}$로부터 $\mathbf{x}^{(k)} - \mathbf{x}^{(k-1)}$ 방향으로 더 많이 이동을 하는 것이 $\bar{\mathbf{x}}$에 좀 더 가까이 다가간다고 할 수 있다. 이러한 아이디어를 적용한 것을 축차가속완화법(SOR 방법)(successive over-relaxation method)이라 한다.
$ $
이제 SOR 방법을 통해 $\hat{\mathbf{x}}^{(k-1)}$를 얻었다 가정하고, $\hat{\mathbf{x}}^{(k-1)}$에 가우스-자이델 방법을 적용하면 \[ \mathbf{x}^{(k)} = D^{-1} \big[ \mathbf{b} - L \mathbf{x}^{(k)} - U \hat{\mathbf{x}}^{(k-1)} \big] \] 을 얻는다. 위 식의 양변에 $\hat{\mathbf{x}}^{(k-1)}$를 빼주고 식을 정리하면 \begin{align*} \mathbf{x}^{(k)} - \hat{\mathbf{x}}^{(k-1)} & = D^{-1} \big[ \mathbf{b} - L \mathbf{x}^{(k)} - U \hat{\mathbf{x}}^{(k-1)} \big] - \hat{\mathbf{x}}^{(k-1)} \\ & = D^{-1} \big[ \mathbf{b} - L \mathbf{x}^{(k)} - (D+U) \hat{\mathbf{x}}^{(k-1)} \big] \end{align*} 을 얻는다. 이제 위 식 우변의 $\mathbf{x}^{(k)}$을 $\hat{\mathbf{x}}^{(k)}$로 바꾼 \[ D^{-1} \big[ \mathbf{b} - L \hat{\mathbf{x}}^{(k)} - (D+U) \hat{\mathbf{x}}^{(k-1)} \big] \] 을 $\hat{\mathbf{x}}^{(k-1)}$로부터 $\hat{\mathbf{x}}^{(k)}$를 얻기 위해 이동해야할 방향으로 설정한다. 따라서 적당한 완화 변수(relaxation parameter) $1 < \omega < 2$에 대하여 \begin{align*} \hat{\mathbf{x}}^{(k)} & = \hat{\mathbf{x}}^{(k-1)} + \omega(\hat{\mathbf{x}}^{(k)} - \hat{\mathbf{x}}^{(k-1)}) \\ & = \hat{\mathbf{x}}^{(k-1)} + \omega D^{-1} \big[ \mathbf{b} - L \hat{\mathbf{x}}^{(k)} - (D+U) \hat{\mathbf{x}}^{(k-1)} \big]. \end{align*} 마찬가지로 벡터 $\hat{\mathbf{x}}^{(k)}$의 $i$번째 성분에 대한 계산을 살펴보면 \[ \hat{x}^{(k)}_i = \hat{x}^{(k-1)}_i + \frac{\omega}{a_{ii}} \Bigg[ b_i - \sum_{j=1}^{i-1} a_{ij}\hat{x}^{(k)}_j - \sum_{j=i}^{n} a_{ij} \hat{x}^{(k-1)}_j \Bigg] \] 를 얻는다.
$ $
이제 SOR 방법에서 $\hat{\mathbf{x}}^{(k)}$에 대한 닫힌 형태의 점화식을 구해보자. 우선 식 \[ \hat{\mathbf{x}}^{(k)} = \hat{\mathbf{x}}^{(k-1)} + \omega D^{-1} \big[ \mathbf{b} - L \hat{\mathbf{x}}^{(k)} - (D+U) \hat{\mathbf{x}}^{(k-1)} \big] \] 의 양변에 $\frac{1}{\omega}D$를 곱하면 \[ \frac{1}{\omega}D \hat{\mathbf{x}}^{(k)} = \frac{1}{\omega}D \hat{\mathbf{x}}^{(k-1)} + \big[ \mathbf{b} - L \hat{\mathbf{x}}^{(k)} - (D+U) \hat{\mathbf{x}}^{(k-1)} \big] \] 이다. 따라서 위 식을 정리하여 \begin{align*} \hat{\mathbf{x}}^{(k)} & = \Big( L + \frac{1}{\omega} D \Big)^{-1} \Big[ \mathbf{b} - \Big( \frac{\omega - 1}{\omega}D + U \Big) \hat{\mathbf{x}}^{(k-1)} \Big] \\[1ex] & = \big( \omega L + D \big)^{-1} \big[ \omega \mathbf{b} - \big( (\omega - 1)D + \omega U \big) \hat{\mathbf{x}}^{(k-1)} \big] \end{align*} 를 얻는다. 이를 통해 $\Norm{(\omega L + D)^{-1} ((\omega - 1)D + \omega U)} < 1$이 성립할 때, 임의의 초기벡터 $\mathbf{x}^{(0)}$에 대한 벡터열 $(\mathbf{x}^{(k)})$가 선형연립방정식의 해로 수렴함을 확인할 수 있다.
$ $
참고. SOR 방법에서 완화 변수 $\omega = 1$인 경우, 가우스-자이델 방법으로 환원된다.$ $
$ $
예제 1.6.1.
Q. 선형연립방정식의 첨가행렬이 다음과 같이 주어졌다고 하자.
\[ [ A \,|\, \mathbf{b} ] = \left[ \, \begin{array}{rrr|r}
4 & 1 & -1 & 4 \\
1 & -4 & 2 & -1 \\
0 & -3 & 4 & 1
\end{array} \, \right] \]
이 때, 초기값을 $\mathbf{x}^{(0)} = (0,\, 0,\, 0)$으로 하고 완화 변수를 $\omega = 1.1$로 하여 SOR 방법을 이용하여 해를 구하여라.
A. MATLAB을 이용하여 $\norm{\mathbf{x}^{(k)} - \mathbf{x}^{(k-1)}} < 0.00001$을 만족할 때까지 SOR 방법을 반복하면,
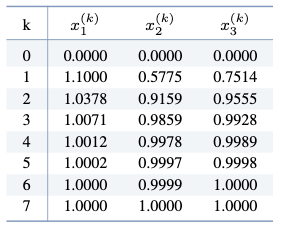가 되어 총 $k=7$번의 SOR 방법의 반복 계산을 통해 $\mathbf{x} =$ $(1,\, 1,\, 1)$이 해가됨을 알 수 있다.$ $
$ $
행렬 $A = [a_{ij}] \in \mathbb{R}^{n \times n}$의 대각성분의 절대값이 그 행의 대각성분을 제외한 나머지 성분의 절대값의 합보다 클 때, 다시 말해 각각의 $i$에 대하여 \[ \abs{a_{ii}} > \sum_{\substack{j = 1 \\ j \neq i}}^{n} \abs{a_{ij}} \] 가 성립할 때, $A$를 강대각지배(strictly diagonally dominant) 행렬이라 한다. 한편, 위 부등식에서 $>$가 $\geq$인 경우, $A$를 대각지배(diagonally dominant) 행렬이라 한다.
$ $
행렬 $A = \begin{bmatrix} 4 & 1 & -1 \\ 1 & -4 & 2 \\ 0 & -3 & 4 \end{bmatrix}$의 경우, \begin{align*} \abs{a_{11}} & = \abs{4} > \abs{1} + \abs{-1} = \abs{a_{12}} + \abs{a_{13}} \\[1ex] \abs{a_{22}} & = \abs{-4} > \abs{1} + \abs{2} = \abs{a_{21}} + \abs{a_{23}} \\[1ex] \abs{a_{33}} & = \abs{4} > \abs{0} + \abs{-3} = \abs{a_{31}} + \abs{a_{32}} \end{align*} 이 모두 성립하므로 $A$는 강대각지배 행렬이다.
$ $
다음 정리는 어떠한 행렬에 대하여 반복법의 수렴성이 보장되는지를 알려준다.
$ $
$ $
참고. $1 < \omega < 2$인 경우, 가속완화(over-relaxation)가 되어 수렴속도가 느린 반복법에서 수렴속도를 향상시키고자 할 때 사용되고, 반대로 $0 < \omega < 1$인 경우 감속완화(under-relaxation)가 되어 반복법이 발산할 때 수렴성을 보장받거나 오버슈팅을 방지하기 위하여 사용된다.$ $
$ $