선형연립방정식 $A\mathbf{x} = \mathbf{b}$에 대하여, 계수행렬 $A \in \mathbb{R}^{n \times n}$가 적당한 행렬 $N,\, P \in \mathbb{R}^{n \times n}$에 대하여 $A = N - P$로 표현되었다고 가정하자. 그러면 주어진 선형연립방정식은 \[ N\mathbf{x} = P\mathbf{x} + \mathbf{b} \] 를 푸는 것과 동치이다.
$ $
$ $
증명. 결론을 부정하여 $A$의 역행렬이 존재하지 않는다고 가정해보자. 그러면 선형연립방정식 $A\mathbf{x} = \mathbf{0}$의 비자명해 $\mathbf{x} \neq \mathbf{0}$가 존재한다. 따라서 \[ A\mathbf{x} = \mathbf{0} \implies N\mathbf{x} = P \mathbf{x} \implies \mathbf{x} = N^{-1}P\mathbf{x} \] 를 차례로 얻는다. 위 마지막 식에 양변에 노름을 취하면 \[ \norm{\mathbf{x}} = \norm{N^{-1}P\mathbf{x}} \leq \Norm{N^{-1}P} \norm{\mathbf{x}} < \norm{\mathbf{x}} \] 가 되어 모순이 생기고, 따라서 $A$의 역행렬이 존재함을 알 수 있다.$ $
$ $
위 보조정리 1.5.1.에 의해 $\Norm{N^{-1}P} < 1$인 경우, 선형연립방정식 $A\mathbf{x} = \mathbf{b}$의 유일한 해 $\bar{\mathbf{x}}$가 존재하고, 따라서 \[ N\mathbf{x} = P\mathbf{x} + \mathbf{b} \] 의 해 또한 $\bar{\mathbf{x}}$가 된다. 이제 초기벡터 $\mathbf{x}^{(0)}$를 임의로 설정하고 $\mathbf{x}^{(k)}$를 다음과 같이 귀납적으로 정의하자. \[ N\mathbf{x}^{(k)} = P \mathbf{x}^{(k-1)} + \mathbf{b}. \] 한편 $N\bar{\mathbf{x}} = P \bar{\mathbf{x}} + \mathbf{b}$가 성립하므로 \[ \begin{align*} N\mathbf{x} - N\mathbf{x}^{(k)} & = \big( P \bar{\mathbf{x}} + \mathbf{b} \big) - \big( P \mathbf{x}^{(k-1)} + \mathbf{b} \big) \\[1ex] & = P \big( \bar{\mathbf{x}} - \mathbf{x}^{(k-1)} \big) \end{align*} \] 이고 위 식을 정리하면 \[ \mathbf{x} - \mathbf{x}^{(k)} = N^{-1} P \big( \bar{\mathbf{x}} - \mathbf{x}^{(k-1)} \big) \] 을 얻는다. 이제 위 식의 양변에 노름을 취하면 \begin{align*} \norm{\mathbf{x} - \mathbf{x}^{(k)}} & = \norm{N^{-1}P \big( \bar{\mathbf{x}} - \mathbf{x}^{(k-1)} \big)} \\[1ex] & \leq \Norm{N^{-1}P} \norm{\bar{\mathbf{x}} - \mathbf{x}^{(k-1)}} \\[1ex] & = \Norm{N^{-1}P} \norm{N^{-1}P \big(\bar{\mathbf{x}} - \mathbf{x}^{(k-2)} \big)} \\[1ex] & \leq \Norm{N^{-1}P}^{2} \norm{\bar{\mathbf{x}} - \mathbf{x}^{(k-2)}} \\ & \;\;\vdots \\ & \leq \Norm{N^{-1}P}^{k} \norm{\bar{\mathbf{x}} - \mathbf{x}^{(0)}} \end{align*} 이다. 이제 $\Norm{N^{-1}P} < 1$이므로 $k \to \infty$의 극한을 취하면 \[ \lim_{k \to \infty} \norm{\bar{\mathbf{x}} - \mathbf{x}^{(k)}} = 0 \] 이 되어 $\mathbf{x}^{(k)}$는 $\bar{\mathbf{x}}$로 수렴함을 알 수 있다.
$ $
$ $
참고. 반복법을 수행하여 $\mathbf{x}^{(k)}$를 계산할 때 $N^{-1}$의 연산이 필요하게 되므로, 역행렬을 쉽게 구할 수 있는 $N$을 택하게 된다.$ $
$ $
참고. 반복법을 사용하여 수치적으로 선형연립방정식의 해를 구하는 경우, $\mathbf{x}^{(k)}$를 구하는 연산을 무한히 반복할 수 없으므로, 언제까지 연산을 반복 수행해야할 것인지 정해주어야 한다. 만약 선형연립방정식의 해 $\bar{\mathbf{x}}$를 알고 있다면, 적당한 $\epsilon > 0$에 대하여 $\norm{\bar{\mathbf{x}} - \mathbf{x}^{(k)}} < \epsilon$이 될 때까지 반복하면 되지만 실제로는 $\bar{\mathbf{x}}$의 값을 알 수 없는 경우가 대부분이다. 따라서
- 미리 설정해 둔 반복 횟수의 최댓값 $k_{\max}$을 이용하여 $k = k_{\max}$일 때까지 반복
- 적당한 $\epsilon > 0$을 설정하여 $\norm{\mathbf{x}^{(k)} - \mathbf{x}^{(k-1)}} < \epsilon$이 될 때까지 반복
또는 위 방법을 함께 사용하여 반복횟수를 조절하게 된다.$ $
$ $
$A = N - P$를 만족하는 행렬 $N,\, P \in \mathbb{R}^{n \times n}$을 선택하는 방법에 따라 야코비 방법(Jacobi method)와 가우스-자이델 방법(Gauss-Seidel method) 등으로 나눌 수 있다.
$ $
행렬 $A \in \mathbb{R}^{n \times n}$의 대각 성분 아래 성분만으로 이루어진 하삼각행렬을 $L$, 대각성분만으로 이루어진 대각행렬을 $D$, 그리고 대각성분 위에 있는 성분만으로 이루어진 상삼각행렬을 $U$라 하면 \[ A = L + D + U \] 와 같이 나타낼 수 있다. 이제 $N = D$, $P = -(L+U)$로 정의하여 반복법을 수행하는 것을 야코비 방법(Jacobi method)이라 한다. 야코비 방법을 적용하면 \[ D \mathbf{x}^{(k)} = \mathbf{b} - (L+U)\mathbf{x}^{(k-1)} \] 또는 위 식을 정리하여 \[ \mathbf{x}^{(k)} = D^{-1} \big[ \mathbf{b} - (L+U)\mathbf{x}^{(k-1)} \big] \] 을 얻는다. 이제 위 식에서 벡터 $\mathbf{x}^{(k)}$의 $i$번째 성분에 대한 계산을 살펴보면, \[ x^{(k)}_i = \frac{1}{a_{ii}} \Bigg[ b_i - \sum_{\substack{j = 1 \\ j \neq i}}^{n} a_{ij} x^{(k-1)}_j \Bigg] \] 가 되어 벡터 $\mathbf{x}^{(k)}$를 쉽게 구할 수 있다. 야코비 방법에서는 $\Norm{D^{-1}(L+U)} < 1$이 성립하면 임의의 초기벡터 $\mathbf{x}^{(0)}$에 대한 벡터열 $(\mathbf{x}^{(k)})$가 실제 선형연립방정식의 해로 수렴한다.
$ $
예제 1.5.3.
Q. 선형연립방정식의 첨가행렬이 다음과 같이 주어졌다고 하자.
\[ [ A \,|\, \mathbf{b} ] = \left[ \, \begin{array}{rrr|r}
4 & 1 & -1 & 4 \\
1 & -4 & 2 & -1 \\
0 & -3 & 4 & 1
\end{array} \, \right] \]
이 때, 초기값을 $\mathbf{x}^{(0)} = (0,\, 0,\, 0)$으로 하고 야코비 방법을 이용하여 해를 구하여라.
A. 야코비 방법을 이용하여 $\mathbf{x}^{(1)},\, \mathbf{x}^{(2)}$를 구해보자.
\begin{align*}
\mathbf{x}^{(1)} & = D^{-1} \big( \mathbf{b} -(L+U)\mathbf{x}^{(0)} \big) \\[1ex]
& = \begin{bmatrix}
\frac{1}{4} & 0 & 0 \\
0 & -\frac{1}{4} & 0 \\
0 & 0 & \frac{1}{4}
\end{bmatrix} \left( \begin{bmatrix} 4 \\ -1 \\ 1 \end{bmatrix} - \begin{bmatrix}
0 & 1 & -1 \\
1 & 0 & 2 \\
0 & -3 & 0
\end{bmatrix} \begin{bmatrix} \,0\,\, \\ 0 \\ 0 \end{bmatrix} \right) \\[1ex]
& = \begin{bmatrix} 1 \\ \frac{1}{4} \\ \frac{1}{4} \end{bmatrix} \\[2ex]
\mathbf{x}^{(2)} & = D^{-1} \big( \mathbf{b} -(L+U)\mathbf{x}^{(1)} \big) \\[1ex]
& = \begin{bmatrix}
\frac{1}{4} & 0 & 0 \\
0 & -\frac{1}{4} & 0 \\
0 & 0 & \frac{1}{4}
\end{bmatrix} \left( \begin{bmatrix} 4 \\ -1 \\ 1 \end{bmatrix} - \begin{bmatrix}
0 & 1 & -1 \\
1 & 0 & 2 \\
0 & -3 & 0 \end{bmatrix} \begin{bmatrix} \,1\,\, \\ \frac{1}{4} \\ \frac{1}{4} \end{bmatrix} \right) \\[1ex]
& = \begin{bmatrix} 1 \\ \frac{5}{8} \\ \frac{7}{16} \end{bmatrix} \eqqed
\end{align*}
$ $
참고. 실제로 MATLAB을 이용하여 $\norm{\mathbf{x}^{(k)} - \mathbf{x}^{(k-1)}} < 0.00001$을 만족할 때까지 야코비 방법을 반복하면,
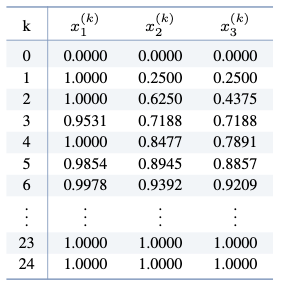 가 되어 총 $k=24$번의 야코비 방법의 반복 계산을 통해 $\mathbf{x} = (1,\, 1,\, 1)$이 해가됨을 알 수 있다.$ $
가 되어 총 $k=24$번의 야코비 방법의 반복 계산을 통해 $\mathbf{x} = (1,\, 1,\, 1)$이 해가됨을 알 수 있다.$ $
$ $