임의의 노름공간(normed vector space) $(X,\, \norm{\cdot})$의 임의의 두 벡터 $x,\, y \in X$에 대하여 다음의 삼각부등식(triangle inequality) 가 성립한다.
\[ \norm{x+y} \leq \norm{x} + \norm{y} \]
그렇다면 위 부등식의 두 항의 크기는 어느정도나 차이가 나는 걸까?
삼각부등식(triangle inequality)의 두항의 크기의 차
다음 정리는 논문 [Lech Maligranda, "Simple Norm Inequalities", The American Mathematical Monthly, Vol. 113, No. 3 (Mar., 2006), pp. 256-260]에서 찾아 볼 수 있다.
정리. (Maligranda, 2006)임의의 노름공간$(X,\, \norm{\cdot})$의 임의의 $0$이 아닌 두 벡터 $x,\, y \in X$에 대하여 다음 부등식이 성립한다.
\[ \norm{x+y} \leq \norm{x} + \norm{y} - \left( 2 - \norm{\frac{x}{\norm{x}} + \frac{y}{\norm{y}}} \right) \min(\norm{x},\, \norm{y}) \tag*{$\myblue{(1)}$} \]
\[ \norm{x+y} \geq \norm{x} + \norm{y} - \left( 2 - \norm{\frac{x}{\norm{x}} + \frac{y}{\norm{y}}} \right) \max(\norm{x},\, \norm{y}) \tag*{$\myblue{(2)}$} \]
또한 $\norm{x} = \norm{y}$이거나 양의 실수 $\alpha>0$에 대하여 $y = \alpha x$일 때, 위 두 부등식에서 등호가 성립한다.
증명. 일반성을 잃지 않고 $0 < \norm{x} \leq \norm{y}$라 하자. 그러면 삼각부등식에 의해
\[ \begin{align*} \norm{x+y} &= \norm{\frac{\norm{x}}{\norm{x}}x + \frac{\norm{x}}{\norm{y}}y + \left( 1 - \frac{\norm{x}}{\norm{y}} \right)y} \\[5px] &\leq \norm{\frac{\norm{x}}{\norm{x}}x + \frac{\norm{x}}{\norm{y}}y} + \norm{\left( 1 - \frac{\norm{x}}{\norm{y}} \right)y} \\[5px] &= \norm{\frac{x}{\norm{x}} + \frac{y}{\norm{y}}} \norm{x} + \left( 1 - \frac{\norm{x}}{\norm{y}} \right) \norm{y} \\[5px] &= \norm{y} + \left( \norm{\frac{x}{\norm{x}} + \frac{y}{\norm{y}}} - 1 \right) \norm{x} \\[5px] &= \norm{x} + \norm{y} + \left( \norm{\frac{x}{\norm{x}} + \frac{y}{\norm{y}}} - 2 \right) \norm{x} \\[5px] &= \norm{x} + \norm{y} - \left( 2 - \norm{\frac{x}{\norm{x}} + \frac{y}{\norm{y}}} \right) \norm{x} \end{align*} \]
를 얻는다. 따라서 부등식 $\myblue{(1)}$이 성립함을 알 수 있다. 마찬가지 방법으로
\[ \begin{align*} \norm{x+y} &= \norm{\frac{\norm{y}}{\norm{x}}x + \frac{\norm{y}}{\norm{y}}y + \left( 1 - \frac{\norm{y}}{\norm{x}} \right)x} \\[5px] &\geq \norm{\frac{\norm{y}}{\norm{x}}x + \frac{\norm{y}}{\norm{y}}y} - \norm{\left( 1 - \frac{\norm{y}}{\norm{x}} \right)x} \\[5px] &= \norm{\frac{x}{\norm{x}} + \frac{y}{\norm{y}}} \norm{y} - \left( \frac{\norm{y}}{\norm{x}} - 1 \right) \norm{x} \\[5px] &= \norm{x} + \left( \norm{\frac{x}{\norm{x}} + \frac{y}{\norm{y}}} - 1 \right) \norm{y} \\[5px] &= \norm{x} + \norm{y} + \left( \norm{\frac{x}{\norm{x}} + \frac{y}{\norm{y}}} - 2 \right) \norm{y} \\[5px] &= \norm{x} + \norm{y} - \left( 2 - \norm{\frac{x}{\norm{x}} + \frac{y}{\norm{y}}} \right) \norm{y} \end{align*} \]
이므로 부등식 $\myblue{(2)}$ 또한 성립한다. 마지막으로 두 부등식의 등호조건은 삼각부등식의 등호조건으로부더 간단히 얻을 수 있다..
각거리(angular distance)
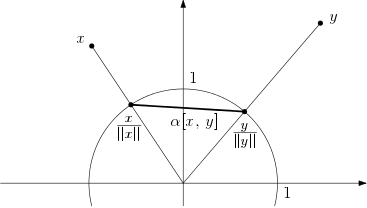
임의의 $0$이 아닌 두 벡터 $x,\, y \in X$에 대하여 $x$와 $y$의 각거리(angular distance) 를 아래와 같이 정의한다.
\[ \alpha[x,\,y] := \norm{\frac{x}{\norm{x}} - \frac{y}{\norm{y}}} \]
위 정의는 기하학적으로 아래와 같이 해석할 수 있다.
기하학적으로 두 점 $x$와 $y$의 각거리는 $x$와 $y$를 단위구 위로 사영한 두 점 사이의 거리로 정의됨을 알 수 있다. 또한 단위구 위의 두 점 사이의 거리의 최댓값은 단위구의 지름의 길이인 $2$이므로 $\alpha[x,\,y] \leq 2$임을 간단히 확인할 수 있다.
참고. 위 각거리의 정의를 이용하여 두 부등식 $\myblue{(1)}$과 $\myblue{(2)}$를 정리하면 삼각부등식의 두 항의 차 $\norm{x} + \norm{y} - \norm{x+y}$에는 다음의 부등식
\[ (2 - \alpha[x,\,-y]) \min(\norm{x},\, \norm{y}) \leq \norm{x} + \norm{y} - \norm{x+y} \leq (2 - \alpha[x,\,-y]) \max(\norm{x},\, \norm{y}) \tag*{$\myblue{(3)}$} \]
가 성립함을 알 수 있다..
두 부등식 $\myblue{(1)}$과 $\myblue{(2)}$로부터 각거리에 대한 상계과 하계를 구할 수 있다.
따름정리. 임의의 노름공간$(X,\, \norm{\cdot})$의 임의의 $0$이 아닌 두 벡터 $x,\, y \in X$에 대하여 다음 부등식이 성립한다.
\[ \frac{\norm{x-y} - \abs{\norm{x} - \norm{y}}}{\min(\norm{x},\, \norm{y})} \leq \alpha[x,\,y] \leq \frac{\norm{x-y} + \abs{\norm{x} - \norm{y}}}{\max(\norm{x},\, \norm{y})} \tag*{$\myblue{(4)}$} \]
또한 $\norm{x} = \norm{y}$이거나 양의 실수 $\alpha>0$에 대하여 $y = \alpha x$일 때, 위 두 부등식에서 등호가 성립한다.
증명. 우선 임의의 두 벡터 $x,\, y \in X$에 대하여 다음 사실이 성립한다.
\[ 2\max(\norm{x},\, \norm{y}) = \norm{x} + \norm{y} + \abs{\norm{x} - \norm{y}} \]
\[ 2\min(\norm{x},\, \norm{y}) = \norm{x} + \norm{y} - \abs{\norm{x} - \norm{y}} \]
위 등식은 $\norm{x} \geq \norm{y}$인 경우와 $\norm{x} \leq \norm{y}$인 경우를 나누어 생각하면 간단히 증명이 가능하므로 생략하도록 하자. 이제 부등식 $\myblue{(2)}$의 양변의 $y$ 대신 $-y$를 대입하여 정리하면
\[ \norm{x-y} \geq \norm{x} + \norm{y} - (2 - \alpha[x,\,y]) \max(\norm{x},\, \norm{y}) \]
를 얻는다. 이제 위 부등식을 정리하면
\[ \begin{align*} \alpha[x,\,y] \max(\norm{x},\, \norm{y}) &\leq \norm{x-y} + 2\max(\norm{x},\, \norm{y}) - \norm{x} - \norm{y} \\[5px] &= \norm{x-y} + \abs{\norm{x} - \norm{y}} \end{align*} \]
부등식 $\myblue{(4)}$의 우변을 얻는다. 마찬가지 방법으로 부등식 $\myblue{(1)}$을 정리하여 부등식 $\myblue{(4)}$의 좌변 또한 얻을 수 있다..