Moreau의 정리 - Math Storehouse

Projection on Closed Convex Sets

$(H,\, \ip{\cdot}{\cdot})$ 를 Hilbert space라 하고 $C \in H$가 closed convex set이라 하자. (집합 $C \in H$가 임의의 $x,\, y \in C$와 $t \in [0,\,1]$에 대하여 $tx + (1-t)y \in C$를 만족할 때, $C$를 convex set이라 한다.) 그러면 $C$ 위로의 projection mapping $P_C : H \to C$를 다음과 같이 정의한다: 임의의 $x \in H$에 대하여, $y = P_C(x)$는 아래 식을 만족하는 해이다.

\[ \norm{x-y} = \min_{z \in C} \norm{x-z}. \]

다시말해 $x$로부터 거리가 최소인 집합 $C$의 점이 정의에 의해 $P_C(x)$가 된다.

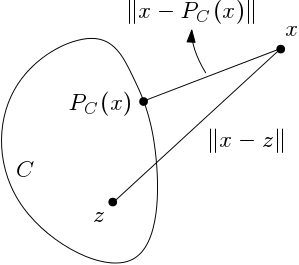
또한 $C$가 closed이고 convex 이므로 임의의 $x \in H$에 대하여 $P_C(x)$가 반드시 존재하고 또 유일함을 쉽게 알 수 있다.

이제 projection을 구하는 또 다른 방법에 대해 알아보자.

정리 1. Obtuse Angle Property

$(H,\, \ip{\cdot}{\cdot})$ 를 Hilbert space라 하고 $C \in H$가 closed convex set이라 하자. $x \in H$와 $y \in C$를 택하자. 그러면 각각의 $y = P_C(x)$이기 위한 필요충분조건은 $y$가 아래의 부등식을 만족하는 것이다.

\[ \ip{x - y}{z - y} \leq 0 \qquad \text{for all $z \in C$}. \]

이 부등식은 obtuse angle property라고도 불리는데, 위 식을 다시 살펴보면 $P_C(x)$가 $x$의 projection이 되기 위한 필요충분조건은 $P_C(x)$가 임의의 $y \in C$에 대하여 $x,\, P_C(x),\, y$로 생성되는 각이 항상 둔각(obtuse angle)을 이루게 해야 함을 알 수 있다.

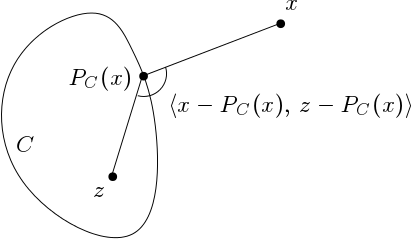
증명. 우선 $y = P_C(x)$라 가정하자. 이제 임의의 $z \in C$와 $t \in (0,\,1)$를 택하자. 그러면 $C$가 convex set이므로, $(1-t)y + tz \in C$임을 알 수 있다. 이제 projection의 정의를 적용하면,

\[ \begin{aligned} \norm{x-y}^2 &\leq \norm{x - [(1-t)y + tz]}^2 \\ &= \norm{x-y - t(z-y)}^2 \\ &= \norm{x-y}^2 - 2t \ip{x-y}{z-y} + t^2 \norm{z-y}^2. \end{aligned} \]

그러므로,

\[ \ip{x-y}{z-y} \leq \frac{t}{2} \norm{z-y}^2. \]

위 식의 양변에 $t \to 0$으로의 극한을 취하면, $\ip{x-y}{z-y} \leq 0$을 얻는다.

이제 역으로 모든 $z \in C$에 대하여, $\ip{x-y}{z-y} \leq 0$을 가정하자. 그러면

\[ \begin{aligned} \norm{x-z}^2 &= \norm{x-y - (z-y)}^2 \\ &= \norm{x-y}^2 - 2 \ip{x-y}{z-y} + \norm{z-y}^2 \\ &\geq \norm{x-y}^2. \end{aligned} \]

따라서 모든 $z \in C$에 대하여 $\norm{x-z} \geq \norm{x-y}$이 성립한다. 따라서 projection의 정의에 의하여, $y = P_C(x)$임을 알 수 있다..

Moreau's Theorem

Moreau의 정리는 주어진 closed convex cone $K \subseteq H$에 대하여, 임의의 점 $x \in H$를 $x$의 $K$와 $K^\circ$ 위로의 projection들의 orthogonal sum으로 나타낼 수 있다는 정리이다.

집합 $K \subseteq H$가 임의의 $x,\,y \in K$와 $\alpha,\, \beta \geq 0$에 대하여, $\alpha x + \beta y \in K$를 만족할 때, $K$를 convex cone이라 한다. 또한 $K$의 polar cone $K^\circ$를 아래와 같이 정의한다.

\[ K^\circ = \set{y \in H}{\ip{x}{y} \leq 0 \text{ for all $x \in K$}}. \]

Moreau의 정리는 아래와 같다.

정리 2. Moreau's Theorem

$K$를 Hilbert space $(H,\, \ip{\cdot}{\cdot})$에서의 closed convex cone이라 하자. 또한 $K^\circ$를 $K$의 polar cone이라 하자. 그러면 임의의 $x,\,y,\,z \in H$에 대하여 다음이 서로 동치이다.

(1) $x \in K$, $y \in K^\circ$이고, $z = x + y$, $\ip{x}{y} = 0$.

(2) $x = P_K(z)$, $y = P_K(z)$.

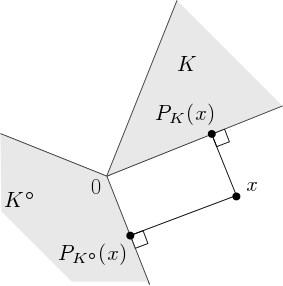
여기서는 위의 Moreau의 정리와 동치형태의 정리를 소개하고 증명해보고자 한다. (사실 원래의 Moreau의 정리가 정리의 모양도 훨씬 깔끔하고 기하학적으로도 자연스럽게 와 닿지만, 실제 optimization 에서는 polar cone보다는 dual cone이 더 중요하게 쓰여지기 때문에 이를 기준으로 Moreau의 정리를 약간 수정하였다.) 우선 closed convex cone $K \subseteq H$에 대하여 $K$의 dual cone $K^*$를 아래와 같이 정의한다.

\[ K^* = \set{y \in H}{\ip{x}{y} \geq 0 \text{ for all $x \in K$}}. \]

그러면, Moreau의 정리는 $K$와 $K^*$를 이용하여 다음과 같이 다시 쓸 수 있다.

정리 3. Moreau's Theorem

$K$를 Hilbert space $(H,\, \ip{\cdot}{\cdot})$에서의 closed convex cone이라 하자. 또한 $K^*$를 $K$의 dual cone이라 하자. 그러면 임의의 $x,\,y,\,z \in H$에 대하여 다음이 서로 동치이다.

(1) $x \in K$, $y \in K^*$이고, $z = x - y$, $\ip{x}{y} = 0$.

(2) $x = P_K(z)$, $y = P_{K^*}(-z)$.

증명. $(1) \Rightarrow (2)$ 우선 $y \in K^*$이므로, 모든 $p \in K$에 대하여 $\ip{y}{p} \geq 0$이고 따라서

\[ \ip{z-x}{p-x} = \ip{-y}{p-x} = -\ip{y}{p} + \ip{y}{x} = - \ip{y}{p} \leq 0. \]

그러므로 obtuse angle property에 의하여 $x = P_K(z)$를 얻는다. 마찬가지로 $x \in K$이므로, 모든 $q \in K^*$에 대하여 $\ip{x}{q} \geq 0$이고

\[ \ip{(-z)-y}{p-y} = \ip{-x}{p-y} = -\ip{x}{p} + \ip{x}{y} = - \ip{x}{p} \leq 0. \]

그러므로 $y = P_{K^*}(-z)$임을 알 수 있다.

$(2) \Rightarrow (1)$ $x = P_K(z)$와 $y = P_{K^*}(-z)$를 가정하자. 먼저 $x = P_K(z)$에 obtuse angle property를 적용하면, 임의의 $p \in K$에 대하여 $\ip{z-x}{p-x} \leq 0$를 얻는다. 특히 $p=0$일 때, $\ip{z-x}{x} \geq 0$이고, $p=2x$일 때, $\ip{z-x}{x} \leq 0$를 얻는다. 따라서 $\ip{z-x}{x} = 0$이여야만 한다. 이제 $w = z-x$라 하자. 그러면, $\ip{w}{x} = 0$임은 자명하고 $y=-w$임을 보이면 증명이 끝난다. 먼저 $-w \in K^*$임을 보이자. 임의의 $p \in K$에 대하여,

\[ \ip{-w}{p} = -\ip{w}{p} = -\ip{w}{p-x} = -\ip{z-x}{p-x} \geq 0 \]

이 성립하므로, $-w \in K^*$임을 알 수 있다. 또한 임의의 $q \in K^*$에 대하여,

\[ \ip{(-z)-(-w)}{q-(-w)} = -\ip{z-w}{q+w} = -\ip{x}{q+w} = -\ip{x}{q} \leq 0 \]

이 성립하므로, $-w = P_{K^*}(-z)$를 얻는다. 이제 projection의 유일성에 의하여 $y=-w$여야만 하고, 따라서 최종적으로 (1)을 얻는다..

References

J. J. Moreau, Décomposition orthogonale d'un espace hilbertien selon deux cones mutuellement polaires, C. R. Acad. Sci., volume 255, pages 238–240, 1962.
Moreau's Decomposition Theorem, Wikimization, last modified 22:07, December 4, 2011.