디랙의 정리(Dirac's Theorem)

      Comments Off on 디랙의 정리(Dirac's Theorem)

어떤 마을에 $n$개의 집이 있다고 하자. 이제 이 마을에 어떤 집에 문제가 생겼을 때 각 집에 이 사실을 알릴 수 있는 비상연락망을 만들고자 한다. 이 때, 비상연락망이란 ABCDEA와 같이 순환적인 연락망 (이 때, 연락망이란 A가 B의 연락처를 알고 B 또한 A의 연락처를 아는 것을 뜻한다.) 이 존재하여 만일 집 C에 문제가 생겨도 DEAB 순으로 서로 연락이 가능해야 함을 뜻한다. 이러한 비상연락망을 만들기 위해서 각 집마다 다른 집의 연락처를 모두 알고 있다면 제일 이상적이겠지만, (비용 또는 보안의 문제 때문에) 각 집에서 알아야 하는 연락처의 개수를 최소화 하고 싶다. 이러한 상황에서 각 집은 최소한 몇개의 다른 집의 연락처를 알아야 할까?

 

만일 $n=5$라 가정해 보자. 만일 모든 집이 적어도 두개의 다른 집의 연락처를 알고 있다면, 아래와 같이 비상연락망이 존재하는 경우, 또는 존재하지 않는 경우가 생긴다.

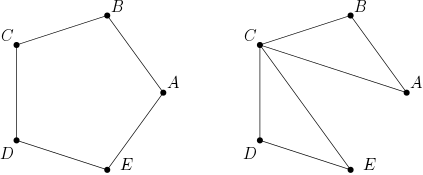
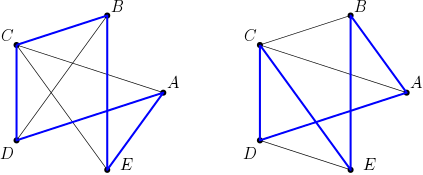
예를 들어 위 그림에서 첫번째 경우, 어떤 집에 문제가 생기더라도 나머지 네개의 집이 서로 연락이 가능하지만, 두번째 경우는, 만약 집 C가 문제가 생긴다면 예를 들어 집 A와 E는 서로 연락할 방법이 없다. 하지만, 모든 집이 적어도 세개의 다른 집의 연락처를 알고 있다면 언제나 비상연락망을 만들 수 있음을 알 수 있다. 아래 그림은 이러한 경우 중 몇가지 예를 보여준다.

이러한 차이가 생기는 이유는 무엇일까? 만약 $n$개의 집이 있다면, 각 집이 최소 몇 개의 다른집의 연락처를 알아야만 언제나 비상연락망을 만들 수 있을까? 이 문제에 대한 해답을 1952년 디랙(Gabriel Andrew Dirac)이 증명하였다. 아래의 디랙의 정리(Dirac's Theorem)와 그 증명을 간단하게 정리해 본다.

 

정리. 디랙의 정리 (Dirac's Theorem)

$G$가 $n \geq e$개의 점을 가진 단순그래프(simple graph)라 하자. 만약 $G$의 모든 점의 차수가 $n/2$ 이상이면, $G$는 해밀턴그래프(Hamiltonian graph)이다. (즉, $G$의 한점에서 출발하여 모든 점을 거쳐 다시 출발점으로 돌아오는 경로가 존재한다.)

 

증명. $E$를 $G$의 모든 변(edge)들의 집합이라 하자. 우선 $G$가 연결그래프(connected graph)임을 보이자. 만약 $G$가 연결그래프가 아니라 가정하고 $G_0$을 $G$의 최소연결성분(minimal connected component)라 하자. 그러면 $G_0$의 최소성에 의해 자명하게 $\abs{G_0}\leq n/2$가 성립한다. 그러면 $G_0$의 점 $p$에 대하여

\[ \operatorname{deg}(p) \leq \abs{G_0} - 1 \leq \frac{n}{2} - 1 \]

이 되어 문제의 가정에 모순이 생긴다.

 

이제 $P = v_1v_2 \cdot v_k$가 $G$에서 최대경로(maximal path)라 하자. 그러면 점 $v_1$와 연결된 모든 점은 집합 $\{v_2,\,v_3,\, \ldots,\, v_k\}$에 속해야만 한다. 만약 그렇지 않다면 (즉, $P$에 속하지 않는 점 $p$가 존재하여 $pv_1 \in E$라면) $pv_1v_2 \cdot v_k$인 경로가 존재하여 $P$의 최대성에 모순이 생기기 때문이다. 또한 $v_1$은 자기 자신과는 인접할 수 없으므로

\[ k \geq \operatorname{deg}(v_1)+1 = \frac{n}{2} +1 \]

이 성립한다. 여기서 $n \geq 3$을 가정했으므로 $k \geq 3$임을 알 수 있다.

 

또한 위와 유사한 논리를 적용하여 $v_k$와 연결된 모든 변은 $\{v_1,\, v_2,\, \ldots,\, v_{k-1}\}$에 속해야 함을 보일 수 있다. 이상의 사실을 다시 표현하면, 적어도 $n/2$개의 $v_i \in \{v_2,\,v_3,\, \ldots,\, v_k\}$는 $v_1v_i \in E$를 만족하고 동시에 적어도 $n/2$개의 $v_i \in \{v_2,\,v_3,\, \ldots,\, v_k\}$는 $v_{i-1}v_k \in E$를 만족한다.

 

여기서 ($v/2 + v/2 = n$개의 변과 $k-1 \leq n-1$개의 점에 대한) 비둘기집의 원리를 적용하면, 적어도 하나의 $v_j \in \{v_2,\,v_3,\, \ldots,\, v_k\}$가 존재하여 $v_1v_j \in E$이고, $v_{j-1}v_k \in E$임을 알 수 있다. 그러면

\[ C = v_1v_jv_{j+1} \cdots v_kv_{j-1}v_{j-2} \cdots v_1 \]

은 순환(cycle)이 된다.

 

다음으로 이 순환 $C$가 해밀턴순환(Hamiltonian cycle)임을, 다시 말해 $k=n$임을 보이자. 만약 $C$에 속하지 않는 점 $p$가 존재한다면, $G$가 연결그래프이므로 어떤 $v_i \in C$가 존재하여 $pv_i \in E$가 성립한다. 하지만 이 경우 $p$와 $C$의 모든 점들을 잇는 경로를 만들 수 있으므로 $P$의 최대성에 모순이 생긴다. 따라서 $G$의 모든 점이 순환 $C$에 속하고 $G$는 해밀턴그래프임을 알 수 있다. .

%nbsp;