지뢰찾기_{(minesweeper)} 게임란 $m \times n$ 크기의 격자에 주어진 숫자를 바탕으로 각 격자에 숨어 있는 지뢰를 모두 찾는 게임이다. 이 때, 각 격자에 주어지는 숫자는 그 격자에 인접한 8개의 격자에 위치한 지뢰의 개수를 나타낸다. 지뢰찾기 게임에도 다양한 수학적 사실이 숨겨져 있는데, 이번 글에서는 그 중 하나를 살펴보도록 하자.

이제 어떤 $m \times n$ 크기의 지뢰찾기 게임이 주어졌다고 하자. 이 게임에서 지뢰가 숨겨져 있는 모든 격자의 지뢰를 없애고, 반대로 지뢰가 숨겨져 있지 않은 모든 격자에 지뢰를 숨기면 새로운 지뢰찾기 게임을 얻게 된다. 이렇게 얻은 게임을 주어진 지뢰찾기 게임의 쌍대_(dual)하고 하자. 예를 들어 아래 두 지뢰찾기 게임은 서로 쌍대 관계이다.

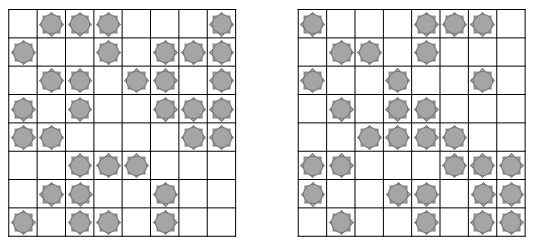
위 두 지뢰찾기 게임에 단서 숫자를 모두 적어보면, 다음을 얻는다.

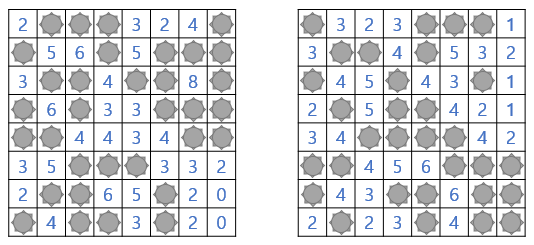
이제 각 지뢰찾기 게임에 주어진 숫자들의 합을 구해보면 두 지뢰찾기 게임 모두 $109$가 됨을 알 수 있다! 이 관찰이 우연일까? 실제로 어떤 $m \times n$ 크기의 두 쌍대 지뢰찾기 게임을 가져오더라도, 이 두 게임에 주어진 숫자들의 합을 각각 구해보면 서로 같음을 확인할 수 있다. 이에 대한 증명은 언뜻 보기에 매우 복잡해야만 할 것 같지만, 실제로는 매우 간단하게 증명할 수 있다. 아래 정리에 대한 내용은 Antonio Jara del las Heras에 의해 처음 발표 되었다고 한다. (American Mathematical Monthly, v116, n3, p227, 2009)

증명. 위 정리를 증명하기 전에, 먼저 다음의 자명한 사실을 살펴보자: $A$를 유한집합이라고 하고, 이 집합 위에 이항관계(binary relation) $R$이 주어졌다고 하자. 이제 $B$와 $C$가 $A$의 부분집합이라 하면, 다음 등식이 성립한다.

이항관계 $R$을 $A \times A$의 부분집합으로 생각하면, 위 등식은 단지 $(B \times C) \cap R$을 서로 다른 두 가지 방법으로 세는 것에 불과하기 때문에 자명하게 등식이 성립함을 알 수 있다.

이제 $(\ast)$을 정리에 적용해 보자. 집합 $A$를 지뢰찾기 게임의 모든 격자들의 집합이라 하고, 두 인접한 격자 $x$와 $y$에 대하여, 이 두 격자 중 오직 하나에만 지뢰가 숨겨져 있으면 $xRy$라 하자. 그러면 자명하게 $R$은 $A$ 위의 이항관계가 된다. 이제 $A$의 부분집합 $B$와 $C$를 각각 지뢰가 숨겨져 있는 모든 격자들의 집합, 지뢰가 숨겨져 있지 않은 모든 격자들의 집합으로 각각 정의하면, $(\ast)$에 의해 정리가 성립함을 알 수 있다..

아래 그림은 두 쌍대 지뢰찾기 게임에서 이항관계에 있는 모든 인접한 두 격자를 붉은 선으로 연결한 것이다.

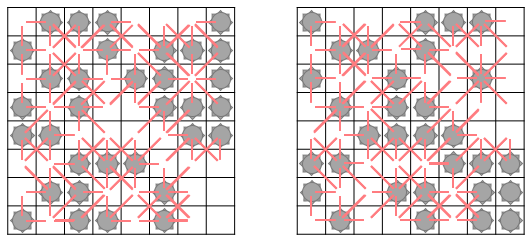
위 그림을 보면 알 수 있듯이 두 쌍대 지뢰찾기 게임에 표시된 붉은 선들이 모두 같음을 알 수 있다. 또한 증명을 보면 알 수 있듯이 이 정리는 어떠한 모양의 지뢰찾기 게임 (예를 들어, 삼각형 또는 육각형 모양의 지뢰찾기 게임) 에도 성립함을 알 수 있다. 나아가 $m \times n$ 크기의 지뢰찾기 게임의 마주보는 변을 연결하여 만든 도넛 모양의 지뢰찾기 게임을 고려하더라도 여전히 이 정리가 성립한다.