풀이 1. 다음과 같이 라그랑지 함수 $L$을 정의하자.
\[ L(x,\,y,\, \lambda) = 15x^2 + 8xy + \lambda(x^2 + y^2 - 4) \]
이제 위 함수를 $x,\,y,\,\lambda$에 대한 편미분을 구하여 $0$으로 두면, 다음의 연립 방정식을 얻는다.
\[ \begin{align} L_x(x,\,y,\,\lambda) &= 30x^2 + 8y + 2x\lambda = 0 \\[5px] L_y(x,\,y,\,\lambda) &= 8x + 2y\lambda = 0 \\[5px] L_{\lambda}(x,\,y,\,\lambda) &= x^2 + y^2 - 4 = 0 \\[5px] \end{align} \]
여기서 $x=0$, $y=0$, 또는 $\lambda=0$인 경우 위 연립 방정식을 만족하지 않음을 간단히 확인할 수 있다. 따라서 $x,\,y,\,\lambda$는 모두 $0$이 아니다. 이제 식 $(2)$로부터 $\lambda = -\frac{4x}{y}$를 얻고 이를 식 $(1)$에 대입하여 정리하면
\[ \begin{align*} 30x + 8y - \frac{8x^2}{y} = 0 &\implies 4y^2 + 15xy - x^2 = 0 \\[5px] &\implies 4 (y+4x) \left( y - \frac{x}{4} \right) = 0 \tag{4} \end{align*} \]
를 얻는다. 따라서 식 $(4)$는 두 직선 $y = -4x$와 $y = \frac{x}{4}$를 나타냄을 알 수 있다. 이제 식 $(3)$과 $(4)$를 연립 하여 계산하면,
$ $
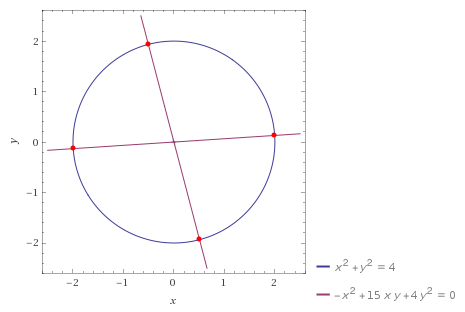
$ $
다음의 네 개의 해를 얻는다.
\[ (x,\,y) = \left( \tfrac{8}{\sqrt{17}},\, \tfrac{2}{\sqrt{17}} \right),\; \left( -\tfrac{8}{\sqrt{17}},\, -\tfrac{2}{\sqrt{17}} \right),\; \left( \tfrac{2}{\sqrt{17}},\, -\tfrac{8}{\sqrt{17}} \right),\; \left( -\tfrac{2}{\sqrt{17}},\, \tfrac{8}{\sqrt{17}} \right) \]
따라서 라그랑지 승수법(Lagrange multiplier method)에 의해 주어진 식의 최댓값 또는 최솟값이 존재하는 점들은 위의 네 점 중에 반드시 포함된다. 이제 위 네 점을 주어진 함수에 대입하여 값을 구해보면,
\[ \begin{align*} \max f(x,\,y) = 64 \quad &\text{when} \; \left( \tfrac{8}{\sqrt{17}},\, \tfrac{2}{\sqrt{17}} \right),\; \left( -\tfrac{8}{\sqrt{17}},\, -\tfrac{2}{\sqrt{17}} \right) \\[5px] \min f(x,\,y) = -4 \quad &\text{when} \; \left( \tfrac{2}{\sqrt{17}},\, -\tfrac{8}{\sqrt{17}} \right),\; \left( -\tfrac{2}{\sqrt{17}},\, \tfrac{8}{\sqrt{17}} \right) \tag*{$\myblue{\blacksquare}$} \end{align*} \]
풀이 2. $x^2 + y^2 - 4 = 0$이므로
\[ \begin{align*} f(x,\,y) &= 15x^2 + 8xy + x^2 + y^2 - 4 \\[5px] &= 16x^2 + 8xy + y^2 - 4 \\[5px] &= (4x+y)^2 - 4 \tag{5} \end{align*} \]
따라서 연립 방정식 $4x+7=0$, $x^2 + y^2=4$를 만족하는 $(x,\,y)$에 대하여, $f$는 최솟값 $-4$를 가진다. 그러므로
\[ \min f(x,\,y) = -4 \quad \text{when} \; \left( \tfrac{2}{\sqrt{17}},\, -\tfrac{8}{\sqrt{17}} \right),\; \left( -\tfrac{2}{\sqrt{17}},\, \tfrac{8}{\sqrt{17}} \right) \]
이제 $f$의 최댓값을 구하기 위하여 식을 좀 더 변형해 보자. 식 $(5)$에 코시-슈바르츠 부등식(Cauchy-Schwarz inequality)를 적용하면,
\[ \begin{align*} f(x,\,y) &= (4x+y)^2 - 4 \\[5px] &\leq (4^2 + 1^2)(x^2 + y^2) - 4 \\[5px] &= 17 \cdot (4) - 4 = 64 \end{align*} \]
위 부등식의 등호 조건은 $(4,\,1)$과 $(x,\,y)$가 일차 종속일 때 이므로 $x=4y$를 얻는다. 따라서 연립 방정식 $x=4y$, $x^2 + y^2=4$를 만족하는 $(x,\,y)$에 대하여, $f$는 최댓값 $-4$를 가진다. 그러므로
\[ \max f(x,\,y) = 64 \quad \text{when} \; \left( \tfrac{8}{\sqrt{17}},\, \tfrac{2}{\sqrt{17}} \right),\; \left( -\tfrac{8}{\sqrt{17}},\, -\tfrac{2}{\sqrt{17}} \right) \tag*{$\myblue{\blacksquare}$} \]
