오늘은 위상수학_(topology)에 대한 일반적인 얘기로 시작해 보려고 한다. 우리가 흔히 학부 수준에서 접하는 위상수학은 사실 일반위상수학_{(general topology)} 또는 점-집합 위상수학_{(point-set topology)}으로 불리는 위상수학의 한 하위 분야로서, 주로 집합의 위상적 성질을 다루는 학문이다. 따라서 누군가가 우리에게 "위상수학은 뭘 공부하는 학문이야?" 라고 물어봤을 때 할수 있는 잘 알려진 대답인, "주어진 대상을 자르거나 붙이지 않고 변화시켜서 다른 대상으로 바꾸어도 변하지 않는 성질들을 연구하는 학문이야." 라고 말하면, 사실 엄밀하게 말하면 반은 맞고 반은 틀린 대답이 된다.

도넛 모양을 자르거나 붙이지 않고 커피컵으로 변화시키는게 가능하다!

위상수학이 이러한 성질들을 연구하는 학문인건 맞지만, 우리가 배우는 일반위상수학은 이러한 성질들을 연구하기 위해 기초를 쌓는 과정으로써 실제로 일반위상수학에서 배우는 불변량은 그리 많지 않기 때문이다. 오히려 일반위상수학은 집합 위에서의 수렴성_{(convergence)}과 연속성_(continuity)을 다루는 학문으로 보는게 더 적절할 지도 모른다. 실제로 일반위상수학에서 분리공간_{(separated space, Hausdorff space)}, 정칙공간_{(regular space)}, 정규공간_{(normal space)} 등을 배우면서 '이런 개념들이 내가 아는 위상수학이랑 무슨 관련이 있는거지?' 하고 고민했던 기억이 난다.

하지만 우선 일반위상수학을 배우고 나면, 일반위상수학의 기초 위에 대수학이나 해석학 등의 기법을 적용하여, 드디어 주어진 대상의 불변량에 대해 공부할 수 있게 된다. 이 때 주어진 대상을 어떠한 관점으로 바라 보는지, 또는 어떠한 기법을 적용하여 연구하는지에 따라 대수적 위상수학_{(algebraic topology)}, 미분 위상수학_{(differential topology)} 등의 하위 분야로 나뉘게 되는 것이다. 따라서 학부 때 배우는 위상수학을 굳이 일반위상수학이라 부르지 않고 간단히 위상수학이라고 부르는 이유도 어떻게 보면 타당한것 같기도 하다.

일반위상수학_{(general topology)}을 처음 배우게 되면 가장 먼저 배우는 개념이 열린 집합_{(open set)}의 개념을 공리화_{(axiomatization)}하여 주어진 집합 $X$의 위상/sub>(topology) $\mathscr{T}$를 정의하는 것이다.

$ $

하지만 왜 하필이면 열린 집합일까? 사실 위의 세가지 조건을 만족하는 $X$의 부분집합들이 왜 열린집합이 되어야 하는지 직관적으로 와닿지도 않는다. 실수상에서 열린구간_{(open interval)} $(a,\,b)$ 들에 대해서 생각해 보자. 그러면 모든 열린구간들의 집합 $\mathscr{I} = \set{(a,\,b)}{a,\,b \in \R}$는 위의 세 가지 공리를 만족 하므로 실수상에서 위상을 이룸을 알 수 있다.

이제 반대로 한번 생각해 보자. 실수상에서 위의 세 가지 공리를 만족하는 실수의 부분집합들의 집합 $\mathscr{T}$에 대해서 생각해 볼 수 있다. 그러면 이 $\mathscr{T}$는 반드시 $\mathscr{I}$가 되어야 할까? 예를 들어 $\mathscr{T} = \{ \emptyset,\, \R \}$이라고 하자. 그러면 단 두개의 원소만으로 이루어진 $\mathscr{T}$는 위상이 되기 위한 세가지 조건을 모두 만족한다! 이러한 공간을 수학에서는 자명 위상공간_{(trivial topological space)} 또는 비이산 위상공간_{(indiscrete topological space)}라고 부른다. 하지만 당연히 $\mathscr{T} \neq \mathscr{I}$임을 알 수 있다. 더욱 이상한 사실은 위상공간 $(\R,\, \mathscr{T})$ 에서는 공집합 $\emptyset$과 전체집합 $\R$을 제외한 모든 부분집합이 열린집합이 아니다! 따라서 열린구간 $(a,\,b)$도 이 위상공간에서는 열린집합이 아니게 된다.

또 다른 예를 한번 생각해 보자. 이번에는 $\mathscr{D}$를 실수 $\R$에서 생각할 수 있는 모든 부분집합을 다 모아놓은 집합이라고 하자. 예를 들면 구간 $[ a,\,b)$나 유리수의 집합 $\mathbb{Q}$, 또는 하나의 실수로만 이루어진 집합 $\{c\}$등이 모두 $\mathscr{D}$의 원소가 된다. 이제, $\mathscr{D}$는 모든 부분집합을 다 포함하고 있으므로, 위상이 되기 위한 세가지 조건을 모두 만족할 수 밖에 없다. 이제 위상공간 $(\R,\, \mathscr{D})$에 대해서 생각해 보자. 이러한 공간을 수학에서는 이산 위상공간_{(discrete topological space)}라 부른다. 이 위상공간에서는 $\R$의 모든 부분집합들이 다 열린집합이 된다. 따라서 $[a,\,b]$와 같은 닫힌구간도 이 위상공간에서는 열린집합이 된다!

위의 두 가지 예만 봐도 알 수 있듯이 (실수 $\R$에서만 보더라도) 열린집합이라는 개념이 우리가 상상하던 열린구간이라는 개념과는 사뭇 다름을 알 수 있다. 그렇다면 왜 하필 위의 세가지 조건을 만족하는 집합의 원소들을 열린집합이라고 하는 것일까? 저 세가지 조건 외에 또 다른 조건을 추가해야 하는 것은 아닐까? 애초에 위상수학을 열린집합의 정의로 부터 시작하는 이유는 무엇일까?

이 질문에 부분적으로나마 대답을 하기 위해서는, 우선 위상수학의 개념이 무엇으로부터 정립되었는지, 그 역사적인 배경을 살펴 볼 필요가 있다.

수학의 출발은 기하학_{(Euclidean geometry)}이다. 세계의 여러 고대 문명에서 농경과 건축을 위해 기하학을 사용하였고, 고대 그리스의 수학자 유클리드의 저서 『원론_(Elements)』에는 유클리드 이전까지 이루어진 모든 기하학의 정수가 담겨져 있다. 그렇다면 기하학은 무엇을 연구하는 학문일까? 당연히 기하학은 주어진 도형의 길이, 넓이, 부피, 각도, 곡률 등의 성질에 대해 다루는 학문이다. 하지만 도형의 색깔, 질감, 냄새, 질량등은 기하학에서 다루지 않는다. 이렇게 기하학에서 다루는 도형의 성질들을 기하학적 성질_{(geometric property)}라 부르는데, 기하학적 성질과 기하학적 성질이 아닌것을 구분하는 기준은 무엇일까?

기하학적 성질들을 자세히 살펴보면 모두 길이_(distance)와 깊게 연관이 있음을 알 수 있다. 도형의 넓이와 부피는 도형에서 측적된 길이로부터 구해지고, 각도가 곡률 또한 길이의 비_(ratio)로써 정의할 수 있다. 좀더 자세히 살펴보기 위해 두 도형의 합동_(congruence)에 대해서 살펴보자. 두 도형 $A$와 $B$가 합동이라는 말은 두 도형의 모양과 크기가 서로 같다는 것을 의미한다.

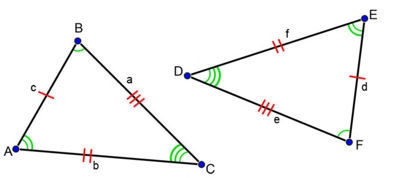
삼각형 $ABC$와 $DEF$는 합동이므로 길이가 보존된다.

합동인 두 도형을 잘 살펴보면 도형 $P$의 임의의 두 점 $x$와 $y$의 사이의 거리와 도형 $Q$의 대응 되는 위치에 있는 두 점 $x'$와 $y'$ 사이의 거리가 항상 같아야 함을 알 수 있다. 좀 더 수학적으로 표현하면, 주어진 두 도형 $P$, $Q$가 합동이려면 전단사함수_{(bijective function)} $f : P \to Q$가 존재하여 임의의 $x,\,y \in P$ 에 대하여, $\abs{x-y} = \abs{f(x)-f(y)}$를 만족해야 한다. 이러한 함수를 등거리변환_(isometry)이라고 한다.

이제, 기하학적 성질을 이러한 등거리변환에 의해서도 변하지 않는 성질이라 정의하자. 그러면 위에 예로 들었던 길이, 넓이, 부피, 각도, 곡률 등의 성질은 모두 등거리변환에 의해서도 변하지 않음을 알 수 있고, 따라서 기하학적 성질이 된다. 이제 등거리변환의 정의를 다시 살펴보면, $\abs{x-y}$라는 표현이 있음을 알 수 있다. 이는 수학적으로 $x$와 $y$ 사이의 거리를 뜻하므로 궁극적으로 기하학은 길이와 관련된 모든것을 다루는 학문이라고 볼 수도 있다. 따라서 먼저 길이 그 자체에 대한 성질이 무엇인지를 알아보는 것이 중요하다. 그러면 몇가지 길이의 성질들에 대해서 알아보자.

$ $

각각의 명제에 대하여, $d(x,\,y) = \abs{x-y}$로 대입만 해보면 전부 간단하게 증명이 된다. 이제 여기서 좀더 나아가 보자. 평면 위의 두 점 사이의 길이뿐만 아니라, 예를 들어 두 행렬 사이의 길이라든지 또는 두 함수 사이의 길이에 대해 생각해 볼 수 있다. 또한 평면 또한 일반적인 집합의 한 예임을 생각해 보면, 나아가 두 집합 사이의 길이 등도 생각해 볼 수 있다. 하지만 이런 경우에 길이를 어떠한 방식으로 정의해야 할까? 따라서 이러한 요구를 모두 충족 시킬 수 있도록 평면 위의 두 점 사이의 길이라는 개념을 자연스럽게 일반화 하면서, 길이가 가져야 하는 필수적인 성질은 잃지 않게끔 길이의 개념을 새롭게 정의할 필요성이 생겨났다.

먼저 다음의 정의를 한번 살펴보자.

$ $

단지 네 가지 성질만을 만족하는 거리공간 $(M,\,d)$로부터 수많은 개념 - 근방_{(neighborhood)}, 열린집합_{(open set)}, 극한_(limit), 연속성_(continuity) 등 - 을 정의할 수 있고, 거리공간의 모든 정리와 증명이 단 네가지 성질로부터 시작된다. 따라서 이 네가지 성질이 거리가 가질 수 있는 수많은 성질 중에서, 깊은 고민과 수많은 다양한 시도 끝에 결정된 거리 개념의 정수일 것이라는 사실을 미루어 짐작해 볼 수 있다.

이제 거리_(metric)의 정의를 잘 살펴보면, 수학적인 표현 방식만 변했을 뿐 길이_(distance)의 첫 네가지 성질과 정확히 일치함을 알 수 있다. 따라서 길이는 거리의 한 특별한 예이다. 성질 (1), (2), (3)은 실생활에서의 거리의 개념을 생각해보면, 너무나 자연스럽게 정의되어 있음을 알 수 있다. (1) 두 원소의 거리는 음수가 될 수 없고, (2) 두 원소가 붙어 있다면 거리는 0이며, (3) 두 원소 사이의 거리는 어느쪽에서 재든 똑같기 때문이다.

하지만 성질 (4)는 무언가 좀 더 특별하고 직관적이지 않아 보인다. 성질 (4)는 흔히 삼각부등식_{(triangle inequality)}이라 불리는 성질인데, 이 성질은 어떠한 두 원소 사이의 거리는 다른 원소를 거쳐서 갈 때의 거리의 합 보다 항상 작아야 함을 보여준다. 하지만 이보다 훨씬 더 중요한 사실이 성질 (4)에 숨겨져 있다. 성질 (4)에 의하면 만약 두 원소 $x$와 $y$ 둘 다 한 원소 $z$에 충분히 가까운 거리에 있다면, $x$와 $y$ 사이의 거리 또한 충분히 작을 수 밖에 없음을 알 수 있다! 누군가는 첫 세가지 성질 (1), (2), (3) 만으로 거리의 개념을 공리화 해보려고 했겠지만, 이 세가지 성질 만으로는 무언가를 정의하고 정리를 증명하는데 제약이 너무 많다. 하지만 성질 (4) 단 하나의 추가 만으로 수학에 커다란 한 분야가 생겨나게 된 것이다.

그런데 왜 하필 이 네가지 성질일까? 성질 (5)나 (6), (7)등을 더 추가하지 않은 이유는 무엇일까? 이 성질들은 앞의 네가지 성질 (1)-(4)로부터는 증명 할 수 없는 독립적인 성질이므로, 만약에 거리가 추가적인 성질을 갖는다면 당연히 더 많은 정리와 증명이 생겨날 것임은 자명하다. 하지만 대답은 이전과 같다.

누군가는 거리의 네가지 성질 (1)-(4) 이외에 (5)나 (6), (7)등의 추가적인 성질까지 만족하는 것만을 거리로써 정의하려고 했겠지만, 그렇게 되면 우리는 거리로 정의할 수 있었던 수많은 후보를 잃어버리게 된다. 그래서 거리가 가질 수 있는 최소한의 하지만 필수적인 성질만을 공리로 설정함으로써 수학을 전개해 나가는 것이다.

드디어 위상수학의 발달 과정에서 열린집합이라는 용어가 처음으로 등장한다. 열린집합이라는 거리공간에서 수열_(sequence)이나 함수_(function)의 수렴성_{(convergence)} 나아가 함수의 연속성_(continuous) 등의 개념 등을 정의하기 위해 필수적인 개념이다. 거리공간에서의 열린집합은 다음와 같이 정의된다.

$ $

이 정의를 착각해서, 열린집합이 아닌 집합을 닫힌집합이라고 생각해서는 안된다. 열린집합이면서 동시에 닫힌집합이 존재하고, 열린집합도 닫힌집하바도 아닌 집합도 존재하기 때문이다! 수학적으로는 표현하면 굉장히 복잡해 보이는 개념이지만 말로 설명하는게 오히려 훨씬 자연스럽게 이해가 된다: $X$의 부분집합 $A$가 열린집합이라는 뜻은 $U$의 임의의 원소 $x$에 대하여, $x$ 주변으로 굉장히 작은 원을 그려서 그 원이 $U$ 안에 언제나 포함되게 할 수 있음을 의미한다.

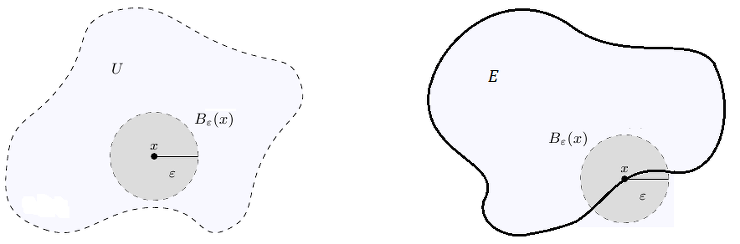
위 그림에서 $U$는 열린 집합이고 $E$는 닫힌집합이다.

위의 그림과 같은 두 집합 $U$와 $E$를 생각해 보자. 이때, 집합 $U$는 경계를 포함하고 있지 않은 반면, $E$는 모든 경계까지 포함하고 있다. 이제 $U$의 임의의 원소 $x$를 생각해 보자. $x$는 $U$ 안에 완전히 포함되어 있기 때문에, $x$ 주변으로 작은 원을 그려 $U$ 안에 완전히 포함되게끔 할 수 있다. 따라서 $U$는 열린 집합이다. 이제 집합 $E$에 대해 생각해 보자. $E$ 내부에 있는 점에 대해서는 작은 원을 그려서 $E$ 안에 포함되게 할 수도 있다. 하지만 $E$의 경계에 있는 점 $x$에 대해서 생각해 보자. 그러면 $x$를 중심으로 아무리 원을 작게 그려도 원의 일부는 집합 $E$의 바깥으로 나오게 된다. 따라서 $E$는 열린집합이 아니다. 하지만 $E$의 여집합은 열린집합이 되므로, $E$는 닫힌집합임을 알 수 있다.

이 열린집합의 개념을 바탕으로 수학에서 가장 중요한 개념중에 하나인 함수의 연속성_(continuity)을 정의할 수 있게 된다.

$ $

하지만, 여기서 문제가 하나 생긴다. 우리에게 임의의 집합 $X$와 $Y$가 있다면, $X$에서 $Y$로 가는 함수 $f$에 대해서 생각해 볼 수 있다. 하지만 이 함수 $f$가 연속임을 어떻게 증명할 수 있을까? 만약에 $X$와 $Y$가 거리공간이라면 문제는 간단하다. 공간 $X$와 $Y$의 거리를 통해 $X$와 $Y$의 열린집합을 정의할 수 있고 이로부터 $f$가 연속함수인지 아닌지를 판단할 수 있기 때문이다. 하지만, 주어진 공간들이 거리공간이 아니라면 어떻게 해야할까? 거리가 없으면 열린집합을 정의할 수 없고 따라서 연속성도 판단할 수가 없다.

주어진 집합 $X$가 거리공간이 아닌 경우에도 열린집합을 정의하는 방법이 있을까? 이 문제를 해결하는 방법은 길이로부터 거리를 정의했을때의 방법과 같다. 열린집합의 다양한 성질들로부터 열린집합이면 반드시 만족해야할 최소한의 성질만을 뽑아 그것을 공리로 지정하고, 그러한 공리를 만족하는 집합을 열린집합이라고 정의하는 것이다.

$ $

마찬가지로 거리공간에서 열린집합이 만족하는 수많은 성질중에서 가장 원초적이면서도 필수적인 성질만을 모아 집합의 위상을 정의하기 위한 공리로 삼아야 한다. 이를 위해 수많은 수학자들의 노력을 하여, 결국 조건 (1), (2), (3)이 그러한 조건임을 알게 되었고, 이것이 위상을 정의하는 세가지 공리가 된 것이다.

마지막으로 일반적인 집합 $X = \{1,,\,2,\,3,\,4\}$와 $Y = \{a,\,b,\,c,\,d\}$ 에서 각각 위상을 정의하고, 두 함수 $f:X \to Y$와 $g:X \to Y$를 정의한 후에 이 함수가 연속인지 아닌지를 보여보자. 먼저 $X$의 위상 $\mathscr{T}$를 다음과 같이 정의하자.

그리고 $Y$의 위상 $\mathscr{S}$는 다음과 같다.

이제 함수 $f:X \to Y$와 $g:X \to Y$를 아래 그림과 같이 정의하자.

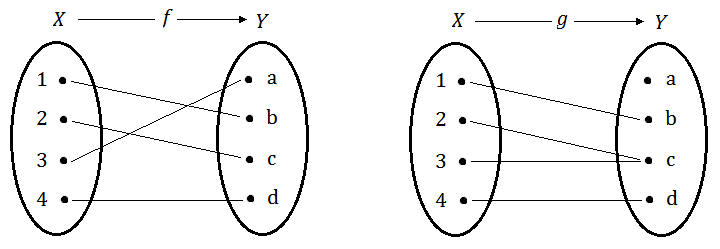
함수$f$는 $3$을 $a$로, 함수 $g$는 $3$을 $c$로 보낸다.

먼저 함수 $f$가 연속함수임을 보이기 위해서는 $\mathscr{S}$의 모든 원소 (열린집합) 들에 대해서, 그 원상이 $\mathscr{T}$의 원소 (열린집합)이 됨을 보여야 한다. 하나씩 살펴 보면, $f^{-1}(\emptyset) = \emptyset$, $f^{-1}(\{a,\,b\}) = \{1,\,3\}$, $f^{-1}(\{c,\,d\}) = \{2,\,4\}$, $f^{-1}(Y) = X$가 된다. 모든 원상들이 $\mathscr{T}$의 원소이므로 함수 $f$는 연속함수임을 알 수 있다. 이제 함수 $g$에 대한 $\mathscr{S}$의 원소들의 원상을 살펴보면, $g^{-1}(\emptyset) = \emptyset$, $g^{-1}(\{a,\,b\}) = \{1\}$, $g^{-1}(\{c,\,d\}) = \{2,\,3,\,4\}$, $g^{-1}(Y) = X$임을 알 수 있다. 하지만, $\{2,\,3,\,4\}$는 $\mathscr{T}$의 원소가 아니다! 따라서 함수 $g$는 연속함수가 아니다.

수학에서 어떠한 대상을 연구하는 방법은 크게 두가지가 있다. 주어진 대상에 적당한 구조가 주어지면 그 자체에 대해서 깊이 연구하는 것이 첫번째 방법이다. 이 방법은 그 대상과 구조가 이미 주어져 있어 상대적으로 이해가 쉽기 때문에 깊이있는 연구를 할 수 있다는 장점이 있지만, 만약에 다른 대상과 다른 구조가 주어지면 기존의 연구 방법이나 정리를 적용하지 못할 수도 있다는 단점이 있다. 두번째 방법은 서로 다른 대상들과 서로다른 구조들에서 공통점을 발견하고 그 공통점만을 모아 공리화 한 뒤, 그 공리화 된 체계 자체를 연구하는 것이다. 이 방법은 구조 자체가 매우 추상적일 수 있어 이해하기도 어렵고 따라서 연구도 쉽지 않지만, 일단 그 체계가 완성이 되면 그 체계에 속하는 모든 대상과 구조에 같은 정리를 적용할 수 있다는 장점이 있다.

아마도 위상수학은 19세기 무렵, 그 당시의 첨단을 달리던 수학자들의 노력이 모여 하나의 잘 만들어진 공리 체계가 수학계 전반에 얼마나 큰 위력을 미칠 수 있는지 보여주는 좋은 사례가 아닐까 싶다.