$\R^3$의 두 벡터 ${\bf u} = (u_1,\, u_2,\, u_3)$와 ${\bf v} = (v_1,\, v_2,\, v_3)$에 대하여 ${\bf u}$와 ${\bf v}$의 외적(cross product) ${\bf u} \times {\bf v}$를 다음과 같이 정의한다.
하지만 이 식을 단순히 외우기는 쉽지 않기 때문에 보통은 선형대수학의 행렬식을 이용하여 다음과 같이 외적을 정의하고는 한다.
행렬식을 이용한 외적의 표현의 장점은 단순히 외적을 외우기 쉽게 도와줄 뿐만 아니라 외적에 대한 여러가지 기본 성질들을 훨씬 간단히 증명할 수 있게 도와준다는데 있다. 간단하게 몇가지 외적의 성질을 증명해 보자.
$ $
$ $
증명. ${\bf u}$와 ${\bf v}$가 한 직선 위에 있으면, 적당한 실수 $k \in \R$에 대하여, ${\bf v} = k{\bf u}$라 할 수 있다. 즉, 행렬식의 한 행이 다른 행의 상수배가 되므로 행렬식의 성질에 의하여 행렬식이 $0$이 되어야 한다. 따라서 ${\bf u} \times {\bf v} = {\bf 0}$이다..
$ $
$ $
증명. ${\bf u} \cdot ({\bf u} \times {\bf v}) = 0$이고 ${\bf v} \cdot ({\bf u} \times {\bf v}) = 0$임을 보이면 충분하다. 이제 세 벡터 ${\bf x}$, ${\bf u}$, ${\bf v}$의 삼중곱(triple product) ${\bf x} \cdot ({\bf u} \times {\bf v})$을 행렬식을 이용하여 다음과 같이 나타낼 수 있다.
위 식에 ${\bf x} = {\bf u}$와 ${\bf x} = {\bf v}$를 각각 대입하면, 행렬식의 성질에 의해 두 경우 모두 $0$이 됨을 확인할 수 있다. 따라서 정리가 성립한다..
$ $
일반적으로 두 벡터 ${\bf u}$와 ${\bf v}$에 모두 수직인 방향는 두개가 존재한다. 하지만 ${\bf u} \times {\bf v}$는 이 두개의 방향 중에 오른손 법칙에 의해 언제나 한쪽 방향을 향한다는 사실이 알려져 있다. 여기서 오른손 법칙(right hand rule)이란 "오른손의 검지의 방향이 ${\bf u}$의 방향을 나타내고 중지의 방향이 ${\bf v}$의 방향을 나타내도록 하면, 엄지가 가르키는 방향이 외적 ${\bf u} \times {\bf v}$의 방향이다"를 말한다.
$ $
사실 외적 ${\bf u} \times {\bf v}$의 방향이 언제나 오른손 법칙을 만족하는 이유는 애초에 외적의 방향이 오른손 법칙을 만족하도록 정의했기 때문이다. 하지만 왜 외적이 오른손 법칙을 만족해야만 하는지는 외적의 정의로부터는 간단히 이해하기는 힘들다. 그래서 이번 글에서는 외적이 오른손 법칙을 언제나 만족함을 증명해 보고자 한다.
$ $
이 증명을 위해서는 먼저 몇 가지 정의가 필요하다. 3차원 공간에서 한 직선 위에 있지 않은 두 벡터 ${\bf u}$와 ${\bf v}$는 평면을 유일하게 결정하고, 이 평면은 3차원 공간을 둘로 나눈다. 이제 이 두 반공간 중에서, 벡터 ${\bf u}$와 ${\bf v}$에 오른손 법칙을 적용했을 때 엄지를 포함하는 쪽의 반공간을 오른쪽 반공간이라 하자.또한 오른쪽 반공간을 $R({\bf u},\, {\bf v})$로 나타내도록 하자.
$ $
마지막으로 두 벡터 ${\bf u}$와 ${\bf v}$에 대하여 오른손 법칙을 만족하는 벡터를 $n({\bf u},\, {\bf v})$로 나타내도록 하자. 이제 어떤 벡터 ${\bf x}$가 ${\bf x} \in R({\bf u},\, {\bf v})$를 만족한다면, ${\bf x}$와 $n({\bf u},\, {\bf v})$가 이루는 각이 예각이여야만 함을 알 수 있다. 아래 그림을 참고하자.
$ $
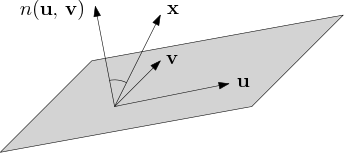
$ $
따라서 오른쪽 반공간을 다음과 같이 정의할 수 있다.
$ $
오른쪽 반공간의 정의를 살펴보면, 어떤 벡터 ${\bf x}$가 두 벡터 ${\bf u}$와 ${\bf v}$에 대하여 오른손 법칙을 만족하면 ${\bf x} \in R({\bf u},\, {\bf v})$지만, 그 역은 성립하지 않음을 알 수 있다. 예를 들어 ${\bf u} = (1,\,0,\,0)$, ${\bf v} = (0,\,1,\,0)$라 하면 $xy$-평면 위쪽 반공간이 오른쪽 공간, $xy$-평면 아래쪽 반공간이 왼쪽 반공간이 되는 식이다. 또한 벡터 ${\bf x} = (0,\,0,\,1)$은 ${\bf x} \in R({\bf u},\, {\bf v})$면서 동시에 오른손 법칙도 만족하지만, 벡터 ${\bf y} = (1,\,1,\,1)$는 ${\bf y} \in R({\bf u},\, {\bf v})$지만 오른손 법칙은 만족하지 않는다.
$ $
이제 다음의 보조정리를 살펴보자.
$ $
$ $
증명. 우선 ${\bf x} \in R({\bf u},\,{\bf v})$를 가정하였으므로, $n({\bf u},\, {\bf v}) \cdot {\bf x} > 0$가 성립한다.
$ $
먼저 (1)을 증명해 보자.
$ $
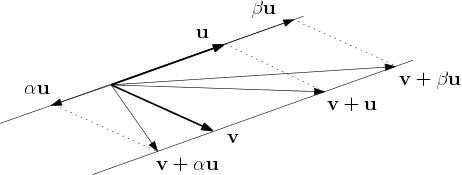
$ $
위 그림에서 확인 할 수 있듯이, ${\bf v}$가 ${\bf v} + \alpha{\bf u}$로 변환 되더라도 검지와 중지의 위치관계는 변하지 않음을 알 수 있다. 따라서 $n({\bf u},\, {\bf v}) = n({\bf u},\, {\bf v} + \alpha{\bf u})$이므로,
이고 따라서 (1)이 성립함을 알 수 있다. 마찬가지 방법으로 (2) 또한 성립한다.
$ $
또한 $n({\bf u},\, {\bf v})$는 ${\bf u}$와 ${\bf u}$에 각각 수직이므로, 임의의 실수 $\alpha,\, \beta \in \R$에 대하여
임을 알 수 있다. 따라서 (3)과 (4) 또한 성립한다.
$ $
마지막으로 (5)를 증명해 보자. 그러면 (6) 또한 같은 방법으로 증명할 수 있다. 세 벡터 $n({\bf x} + \alpha{\bf u},\, {\bf v})$, $n({\bf u},\, {\bf v})$, $n({\bf x},\, {\bf v})$가 모두 벡터 ${\bf v}$에 수직이므로, 이 세 벡터들은 모두 한평면에 존재한다. 따라서 적당한 함수 $f,\,g$를 이용하여
와 같이 나타낼 수 있다. 그럼 우선 $f(0) = 1$, $g(0) = 0$이 성립한다. 또한 오른손 전체를 아주 약간 움직이면 엄지가 가르키는 방향 또한 아주 약간 움직이게 되므로 $f$와 $g$ 모두 연속함수임을 알 수 있다. 이제 어떤 실수 $\alpha$에 대하여 $f(\alpha) < 0$이 성립한다고 가정해보자. 그러면 $f(0) = 1 > 0$이고 $f(\alpha) < 0$이므로, 중간값 정리(intermediate value theorem)에 의해 $f(\beta) = 0$을 만족하는 실수 $\beta$가 존재한다. 따라서
\[ \begin{align*} n({\bf x} + \beta{\bf u},\, {\bf v}) &= f(\beta) n({\bf u},\, {\bf v}) + g(\beta) n({\bf x},\, {\bf v}) \\[5px] &= g(\beta) n({\bf x},\, {\bf v}) \end{align*} \]
를 얻는다. 그러므로 벡터 $n({\bf x} + \beta{\bf u},\, {\bf v})$는 동시에 세 벡터 ${\bf x} + \beta{\bf u}$, ${\bf x}$, ${\bf v}$에 수직이여야 한다. 하지만 이는 모순이므로 모든 실수 $\alpha$에 대하여 $f(\alpha) > 0$을 만족해야 함을 알 수 있다. 그러므로
\[ \begin{align*} n({\bf x} + \alpha{\bf u},\, {\bf v}) \cdot {\bf x} &= \big[ f(\alpha) n({\bf u},\, {\bf v}) + g(\alpha) n({\bf x},\, {\bf v}) \big] \cdot {\bf x} \\[5px] &= \underbrace{f(\alpha)}_{>0} \big[ \underbrace{n({\bf u},\, {\bf v}) \cdot {\bf x}}_{>0} \big] + g(\alpha) \big[ \underbrace{n({\bf x},\, {\bf v}) \cdot {\bf x}}_{=0} \big] \\ &> 0 \end{align*} \]
따라서 (5)가 성립한다. 마찬가지 방법으로 (6) 또한 성립한다..
$ $
위 보조정리를 이용하여 다음 정리를 증명해 보자. 먼저 세 벡터 ${\bf x}$, ${\bf u}$, ${\bf v}$의 삼중곱(triple product) ${\bf x} \cdot ({\bf u} \times {\bf v})$의 행렬식을 이용한 표현
을 상기하자. 다음 정리는 ${\bf x} \in R({\bf u},\,{\bf v})$와 삼중곱 ${\bf x} \cdot ({\bf u} \times {\bf v})$ 사이의 관계를 보여준다.
$ $
$ $
증명. 보조정리에 의해서 세 벡터 중에 하나를 상수배하여 다른 벡터에 더해주어도 여전히 위 관계가 성립함을 알고 있다. 또한 행렬의 한 행을 상수배하여 다른 행에 더해주어도 행렬식의 값은 변하지 않는다. 이제 행렬의 한 행을 상수배하여 다른 행에 더해주는 과정을 적당히 반복하면 주어진 행렬을 다음과 같이 단위행렬로 변환할 수 있고 이 두 행렬의 행렬식은 같다.
또한 ${\bf x} \in R({\bf u},\,{\bf v})$라는 사실과 $a{\bf i} \in R(b{\bf j},\,c{\bf k})$라는 사실은 보조정리에 의해 서로 동치이다. 마지막으로 실제로 오른손 법칙을 이용해서 몇 가지 경우를 나누어 살펴보면 $a{\bf i} \in R(b{\bf j},\,c{\bf k})$일 필요충분조건은 $a{\bf i} \cdot (b{\bf j} \times c{\bf k}) > 0$임을 확인할 수 있다. 따라서 주어진 정리가 성립한다..
$ $
마지막으로 정리 2와 정리 3을 종합하면 우리가 원하는 최종 결과를 얻는다.
$ $
$ $
증명. 먼저 세 벡터 ${\bf u} \times {\bf v}$, ${\bf u}$, ${\bf v}$의 삼중곱은
으로 언제나 양수이다. 따라서 정리 3에 의해서 ${\bf u} \times {\bf v} \in R({\bf u},\,{\bf v})$임을 알 수 있다. 그리고 정리 2에 의해서 ${\bf u} \times {\bf v}$는 두 벡터 ${\bf u}$와 ${\bf v}$에 각각 수직이므로 ${\bf u} \times {\bf v}$의 방향은 오른손 법칙을 따른다..
$ $