이전 글에서 임의로 섞인 루빅스 큐브를 맞추는데 필요한 최소한의 회전수, 즉, 신의 수(God's number)는 20이라는 사실에 대해 살펴 보았다. 이제 조금 관점을 바꾸어서 생각해 보자. 어떤 공식을 단순히 반복 적용하여 (약 4,300경 가지의) 임의의 큐브 배열을 모두 맞출 수 있는 공식이 존재할까? 이제 "(약 4,300경 가지의) 임의의 큐브 배열에 대하여, 단순히 반복 적용하기만 하면, 공식을 적용하는 중간에 큐브를 언제나 맞출 수 있는 공식"을 악마의 공식(devil's number)라 하고, "악마의 공식 중에서 길이가 가장 짧은 공식의 길이"를 악마의 수(devil's number)라 하자.
$ $
먼저 악마의 공식이 존재한다는 사실은 '이론적으로'는 간단히 증명이 가능하다.
$ $
먼저 임의의 큐브 배열을 언제나 20회전 이하로 맞출 수 있음을 알고 있다. 즉, 약 4300경 개의 각각의 큐브 배열에 대하여 이 배열을 맞추는 20회전 이하의 공식이 존재한다는 뜻이다. 이제 임의의 큐브 배열이 주어졌다고 하자. 먼저 (약 4300경 개의 공식 중) 하나의 공식을 사용해 본다. 만약에 큐브가 맞추어 졌다면 멈추고, 큐브가 맞추어 지지 않았다면 방금 썼던 공식의 역공식을 사용해 다시 큐브를 원래의 배열로 돌린다. 이제 방금 전에 썼던 공식을 제외한 다른 공식을 사용하여, 만약 큐브가 맞춰졌다고 멈추고, 맞추어 지지 않았다면 다시 역공식을 쓰는 작업를 반복한다. 이 작업은 유한하므로, 결국 언젠가는 큐브를 맞출 수 있게 된다..
$ $
하지만 이 악마의 공식의 문제점은 (당연하게도) 공식의 길이가 엄청나게 길다는 점에 있다. 단순계산으로도 이 공식의 길이가
약 17해 정도나 된다는 사실을 알 수 있다. 하지만 모든 배열을 맞추는데 20회전이 필요한 것은 아니다. 이전 글을 참고하면 각 큐브의 배열을 맞추는데 필요한 회전수를 대략이나마 알고 있으므로, 이를 이용하여 계산하면, 약 15해 정도로 길이를 줄일 수는 있지만, 여전히 실제로 적용하기는 불가능한 길이의 공식이다. 좀더 나은 방법은 없을까? 아래와 같이 생각해 보자.
$ $
큐브의 모든 배열들의 집합 군(group)을 이룬다. 이 군은 유한군(finite group)이기 때문에, (큐브를 다 맞춘 상태에서) 어떤 공식이든지 이를 반복 적용하면 결국에는 다시 맞춰진 상태로 돌아가게 된다. 예를 들어 공식 $F$의 경우, 4번을 반복하면 총 4번의 상태 변화를 거쳐 다시 원래의 상태로 돌아가게 된다. 또한 공식 $R\; U\; R'\; U'$의 경우, 총 6번을 반복하면, 24번의 상태 변화를 거쳐 다시 원래의 상태로 돌아가게 된다. 주어진 공식을 반복 적용한 횟수를 그 공식의 차수(order)이라 하는데, 예를 들어 공식 $F$는 차수가 4이고, 공식 $R\; U\; R'\; U'$는 차수가 6이 된다. 아직까지 악마의 수에 대해서는 밝혀진 사실이 별로 없지만, 이 수의 상계와 하계에 대해서는 생각해 볼 수 있다.
$ $
cuBer Bruce (http://bruce.cubing.net/)는 2011년과 2012년에 2x2x2 큐브와 3x3x3 큐브의 해밀턴 회로(Hamiltonian cycle)가 존재함을 증명하였다. 약 4300경 개의 큐브 배열을 점으로 생각하고, 어떤 배열에서 다른 배열을 1회전으로 만들 수 있으면, 이 배열을 나타내는 두 점을 선으로 잇는다. 그러면 매우 거대한 점과 선들의 집합이 생길 것이다. 이 때, 이 집합의 선들을 반복해서 지나지 않고 모든 점들을 꼭 한번씩 지나가 다시 시작점으로 돌아오는 경로를 해밀턴 회로라 한다.
$ $
$ $
증명. 앞서 살펴 보았듯이 3x3x3 큐브의 해밀턴 회로가 존재한다는 사실을 알 고 있다. 이 해밀턴 회로를 공식 $H$라 하자. $H$는 큐브의 모든 배열을 정확히 한번씩 포함하기 때문에, 어떤 배열이든지 공식 $H$를 적용하는 도중에 (또는 최악의 경우에도 완전히 적용하고 나면) 맞춰진 배열이 나타나게 된다. 즉, $H$는 악마의 공식이고 이 공식의 길이는 전체 큐브의 배열의 개수인 43,252,003,274,489,856,000이다..
$ $
$ $
증명. 루빅스 큐브의 임의의 공식의 차수에 대한 상한은 1260임을 먼저 보일 것이다. 하지만 이에 대한 증명은 군론(group theory)의 지식을 요하므로 간단히 증명의 개요만 살펴 보도록 하자. 루빅스 큐브에 공식을 적용한다는 것은 루빅스 큐브에 배열을 바꾸는 것으로 이해할 수 있다. 이 때, 임의의 루빅스 큐브의 배열은 '12개 엣지 조각의 위치', '8개 코너 조각의 위치', '12개 엣지 조각의 방향', 그리고 '8개 코너 조각의 방향'의 네 가지 배열의 합성으로 이해할 수 있다. 먼저 '12개 엣지 조각의 위치'에 대하여 얻을 수 있는 가장 큰 차수는 $2 \times 3 \times 7 = 42$이다. 또한 '8개 코너 조각의 위치'에 대하여 얻을 수 있는 가장 큰 차수는 $3 \times 5 = 15$이다. 따라서 '큐브 조각의 위치'에 대하여 얻을 수 있는 가장 큰 차수는 $\operatorname{lcm}(42,\, 15) = 210$이 된다. 여기에 '12개 엣지 조각의 방향'에서 $2$를 곱하고, '8개 코너 조각의 방향'에서 $3$을 추가로 곱해줄 수 있게 되어, 결국 차수에 대한 상한은 $210 \times 2 \times 2 = 1260$이 된다.
$ $
실제로 차수가 1260인 공식이 존재한다. 예를 들어 아래의 공식은 정확히 1260번을 적용해야만 처음의 배열로 돌아간다.
$ $
이제 길이가 $n$인 악마의 공식 $L$에 대해 생각해 보자. 공식 $L$의 차수는 최대 1260이므로 공식 $L$을 반복 적용한다면 최대 $1260n$ 가지의 서로 다른 큐브의 배열을 해결할 수 있다. 하지만 큐브의 모든 배열의 가짓수는 43,252,003,274,489,856,000이기 때문에,
를 얻는다. 따라서 악마의 수는 적어도 34,326,986,725,785,600 이상 이어야만 한다..
$ $
좀 더 간단한 2x2x2 큐브의 경우의 경우를 고려하더라도 악마의 수에 대해 알려진 사실은 거의 없다. 위에서 3x3x3 큐브의 상계와 하계를 찾았던 것과 같은 논리로 생각해 보면, 2x2x2 큐브의 악마의 수의 상계는 3,674,160이고 (이 수는 2x2x2 큐브가 가질수 있는 모든 배열의 수와 같다.) 악마의 수의 하계는 102,060이라는 사실을 보일 수 있다. (이는, 2x2x2 큐브의 공식의 최대 차수가 36이라는 사실로 부터 증명할 수 있다.) cuBer Bruce가 발견한 2x2x2 큐브의 헤밀턴 회로를 살펴 보면 처음 787,320 회전과 바로 다음 787,320 회전이 반복됨을 확인할 수 있다. 따라서 첫 787,320 회전을 제외한 2,866,840이 2x2x2 큐브의 악마의 수의 좀 더 나은 상계가 된다.
$ $
이제 가장 간단한 경우를 살펴 보자. 2x2x2 큐브에서 주어진 면을 180도를 돌리는 하프 턴(half turn)만을 허용한다면, 이렇게 제한된 2x2x2 큐브는 오직 24가지의 서로 다른 배열만을 가진다. 아래 그래프는 각각의 24개의 배열이 어떻게 연결되어 있는지를 보여준다. 아래 그림에서 빨간 선분은 $R^2$, 파란 선분은 $U^2$, 그리고 초록 선분은 $B^2$을 각각 나타낸다. 또한 주어진 두 점이 빨간 선분으로 연결되어 있다고 하면, 두 점 중, 한 점에 해당되는 배열에서 $R^2$ 회전을 하면 다른 점에 해당되는 배열을 얻을 수 있다는 뜻이다.
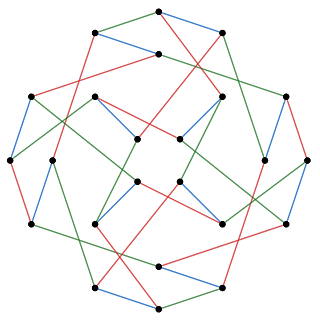
이 경우 무차별 대입(brute force search)를 통해서 악마의 공식과 악마의 수를 찾을 수 있는데, 이는 다음과 같다. \[ R^2 \; U^2 \; R^2 \; U^2 \; R^2 \; B^2 \; R^2 \] 실제로 위 그래프의 어떤 점에서 시작하더라도, 위 공식을 따라서 경로를 그리다 보면 모든 점을 지나 결국 다시 시작점으로 돌아옴을 알 수 있다. 따라서 제한된 2x2x2 큐브의 악마의 수는 7이다.