이번 글에서는 다음과 같이 다항함수를 지수함수로 나눈 형태의 무한급수들
\[ \sum_{n=0}^{\infty} \frac{n}{2^n}, \quad \sum_{n=0}^{\infty} \frac{n^2-3n+2}{4^{n+1}}, \quad \sum_{n=1}^{\infty} \frac{(n-2)^3}{(-3)^n} ,\, \ldots \]
의 값을 구하는 일반적인 방법에 대하여 알아볼 것이다. 이를 위해서 먼저 다음의 정의가 필요하다.
$ $
정의. 주어진 다항식 $p(x)$와 음이 아닌 자연수 $k \geq 0$에 대하여, $\Delta(p\,;\, k,\, x)$를 다음과 같이 정의한다.
\[ \begin{align*}
\Delta(p\,;\,0,\, x) &= p(x), \quad \forall \, x \in \R \\[5px]
\Delta(p\,;\,k,\, x) &= \Delta(p\,;\,k-1,\, x+1) - \Delta(p\,;\,k-1,\, x) \quad \forall \, k \in \N,\, x \in \R
\end{align*} \]
또한 표기상 혼동이 없을때에는 $\Delta(p\,;\, k,\, x)$ 대신에 간단히 $\Delta(k,\, x)$를 쓰기로 한다.
$ $
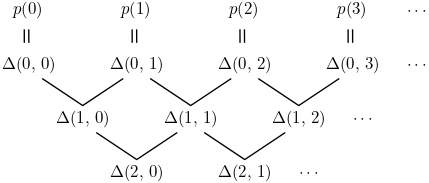
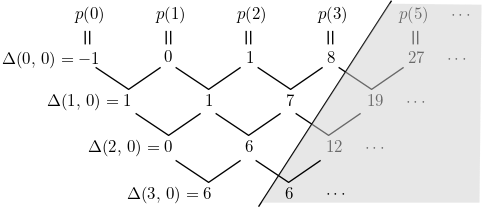
위 정의 자체는 복잡해 보이지만, $x = 0,\, 1,\, 2,\, \ldots$인 경우에 한정해서 보면, 수열 $(p(0),\, p(1),\, p(2),\, \ldots)$의 계차수열들을 반복적으로 구해 나가는 것을 수학적으로 표현한 것에 불과하다. 아래 그림을 보면 $\Delta(k,\, x)$의 정의가 더 직관적으로 와 닿을 것이다.
$ $
$ $
다항함수/지수함수 형태로 이루어진 무한급수의 값
논의를 진행하기에 앞서, $\Delta(k,\, x)$의 성질을 먼저 알아보자.
$ $
보조정리. $d$차 다항함수 $p(x)$에 대하여, 다음 사실들이 성립한다.
$0 \leq k \leq d$에 대하여, $\Delta(k,\, x)$은 $d-k$차 다항함수이다.
특히, $\Delta(d,\, x)$은 상수함수이고 $k \geq d+1$인 경우, $\Delta(k,\, x) = 0$이다.
$q(x) := \Delta(p\,;\, k,\, x)$라 하자. 그러면, $\Delta(q\,;\, 1,\, x) = \Delta(p\,;\, k+1,\, x)$가 성립한다.
$ $
정리. $d$차 다항함수 $p(x)$와 $\abs{a} > 1$을 만족하는 실수 $a \in \R$에 대하여, 다음 등식이 성립한다.
\[ S := \sum_{n=0}^{\infty} \frac{p(n)}{a^{n+1}} = \sum_{k=0}^{d} \frac{\Delta(k,\, 0)}{(a-1)^{k+1}} \tag*{$\myblue{(\ast)}$}\]
$ $
증명. 등식 $\myblue{(\ast)}$를 $p(x)$의 차수에 대한 수학적 귀납법으로 증명을 할 것이다. 우선 $d = 0$인 경우, $p(x) = a_0$라고 둘 수 있고, 이 경우 $\Delta(0,\, 0) = a_0$이므로
\[ \begin{align*}
&\sum_{n=0}^{\infty} \frac{p(n)}{a^{n+1}}
= a_0 \sum_{n=0}^{\infty} \frac{1}{a^{n+1}} = a_0 \cdot \frac{\tfrac{1}{a}}{1 - \tfrac{1}{a}} = \frac{a_0}{a-1} \\[5px]
&\sum_{k=0}^{0} \frac{\Delta(k,\, 0)}{(a-1)^{k+1}}
= \frac{\Delta(0,\, 0)}{a-1} = \frac{a_0}{a-1}
\end{align*} \]
을 얻는다. 따라서 $d=0$인 경우 등식 $\myblue{(\ast)}$이 성립한다.
$ $
이제 등식 $\myblue{(\ast)}$이 $p(x)$의 차수가 $d-1$일 때 성립한다고 가정하자. 이제 차수가 $d$인 $p(x)$에 대하여
\[ a S = \sum_{n=0}^{\infty} \frac{p(n)}{a^n}
= \sum_{n=-1}^{\infty} \frac{p(n+1)}{a^{n+1}}
= p(0) + \sum_{n=0}^{\infty} \frac{p(n+1)}{a^{n+1}} \]
이 성립하므로,
\[ (a-1)S = p(0) + \sum_{n=0}^{\infty} \frac{p(n+1) - p(n)}{a^{n+1}}
= \Delta(0,\, 0) + \sum_{n=0}^{\infty} \frac{\Delta(1,\, n)}{a^{n+1}} \]
을 얻는다. 여기서 $q(x) := \Delta(1,\, x)$라고 두면, $q(x)$는 보조정리 에 의하여 차수가 $d-1$인 다항함수이고, $\Delta(q\,;\, k,\, x) = \Delta(p\,;\, k+1,\, x)$이 성립한다. 따라서 귀납법 가정에 의해
\[ (a-1)S = \Delta(0,\, 0) + \sum_{n=0}^{\infty} \frac{\Delta(1,\, n)}{a^{n+1}}
= \Delta(0,\, 0) + \sum_{k=0}^{d-1} \frac{\Delta(k+1,\, 0)}{(a-1)^{k+1}} \]
이제 위 식의 양변을 $(a-1)$로 나누어 주면,
\[ S = \frac{\Delta(0,\, 0)}{a-1} + \sum_{k=0}^{d-1} \frac{\Delta(k+1,\, 0)}{(a-1)^{k+2}}
= \frac{\Delta(0,\, 0)}{a-1} + \sum_{k=1}^{d} \frac{\Delta(k,\, 0)}{(a-1)^{k+1}}
= \sum_{k=0}^{d} \frac{\Delta(k,\, 0)}{(a-1)^{k+1}} \]
따라서 수학적 귀납법에 의해 정리가 성립한다.$ $
$ $
정리의 활용
이제 몇 가지 예제를 통해서 위 정리를 어떻게 이용할 수 있는지 확인해 보자.
$ $
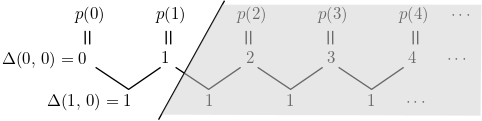
예제 1. 다음 무한급수 $\displaystyle \sum_{n=0}^{\infty} \frac{n}{2^n}$의 값을 구해보자. 우선 $p(x) = x$로 두면 $p(x)$는 $d=1$차 다항함수이므로, $\Delta(0,\, 0)$과 $\Delta(1,\, 0)$의 값만 알면 충분하다. 실제로 간단한 계산을 통해
$\Delta(0,\, 1) = \Delta(1,\, 1) = 1$을 얻는다. (위 그림에서 알 수 있듯이 오직 $p(0),\, p(1)$의 값만 구하면, 필요한 모든 $\Delta(k,\, 0)$의 값을 구할 수 있다.) 이를 위 정리에 적용하면
\[ \sum_{n=0}^{\infty} \frac{n}{2^n} = 2 \sum_{n=0}^{\infty} \frac{n}{2^{n+1}} = \sum_{k=0}^{1} \frac{\Delta(k,\, 0)}{(2-1)^{k+1}}
= 2 \left( \frac{\Delta(0,\, 0)}{2-1} + \frac{\Delta(1,\, 0)}{(2-1)^2} \right) = 2(0 + 1) = 2 \]
를 얻는다. 이 급수에 대한 또 다른 재미있는 사실은 다음글 "두 무한급수의 합 "에서 확인할 수 있다.$ $
$ $
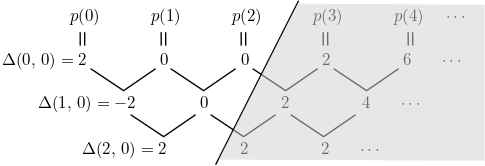
예제 2. 다음 무한급수 $\displaystyle \sum_{n=0}^{\infty} \frac{n^2-3n+2}{4^{n+1}}$의 값을 구해보자. 우선 $p(x) = x^2-3x+2$는 $d=2$차 다항함수이고,
를 얻는다. (실제 계산에서는 $p(0),\, p(1),\, p(2)$의 값만 있으면 충분하다.) 따라서 이를 위 정리에 적용하면
\[ \begin{align*}
\sum_{n=0}^{\infty} \frac{n^2-3n+2}{4^{n+1}}
&= \frac{\Delta(0,\, 0)}{4-1} + \frac{\Delta(1,\, 0)}{(4-1)^2} + \frac{\Delta(2,\, 0)}{(4-1)^3} \\[5px]
&= \frac{2}{3} + \frac{-2}{9} + \frac{2}{27} = \frac{14}{27}
\end{align*} \]
를 얻는다.$ $
$ $
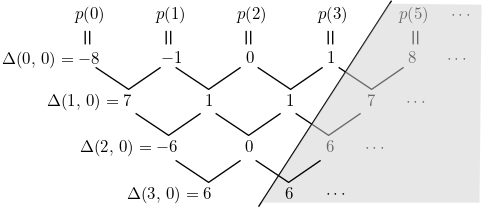
예제 3. 다음 무한급수 $\displaystyle \sum_{n=1}^{\infty} \frac{(n-2)^3}{(-3)^n}$의 값을 구해보자. $p(x) = (x-2)^3$으로 두면 $p(x)$의 차수는 $d=3$이고,
를 얻는다. 따라서 위 정리에 의해
\[ \begin{align*}
\sum_{n=1}^{\infty} \frac{(n-2)^3}{(-3)^n}
&= 8 - 3 \sum_{n=0}^{\infty} \frac{(n-2)^3}{(-3)^{n+1}} \\[5px]
&= 8 - 3 \left( \frac{\Delta(0,\, 0)}{-3-1} + \frac{\Delta(1,\, 0)}{(-3-1)^2} + \frac{\Delta(2,\, 0)}{(-3-1)^3} + \frac{\Delta(3,\, 0)}{(-3-1)^3} \right) \\[5px]
&= 8 - 3 \left( \frac{-8}{-4} + \frac{7}{16} + \frac{-6}{-64} + \frac{6}{256} \right) = \frac{43}{128}
\end{align*} \]
임을 알 수 있다.$ $
$ $
예제 4. 위 예제와 동일한 무한급수 $\displaystyle \sum_{n=1}^{\infty} \frac{(n-2)^3}{(-3)^n}$의 값을 다른 방법으로 구해보자. 먼저 $n = m+1$로 치환하면,
\[ \sum_{n=1}^{\infty} \frac{(n-2)^3}{(-3)^n} = \sum_{m=0}^{\infty} \frac{(n-1)^3}{(-3)^{m+1}} \]
이므로 $d=3$차 다항식 $p(x) = (x-1)^3$을 정의하고 필요한 $\Delta(k,\, 0)$의 값을 구하면
를 얻는다. 그러므로
\[ \begin{align*}
\sum_{m=0}^{\infty} \frac{(n-1)^3}{(-3)^{m+1}}
&= \frac{\Delta(0,\, 0)}{-3-1} + \frac{\Delta(1,\, 0)}{(-3-1)^2} + \frac{\Delta(2,\, 0)}{(-3-1)^3} + \frac{\Delta(3,\, 0)}{(-3-1)^3} \\[5px]
&= \frac{-1}{-4} + \frac{1}{16} + \frac{0}{-64} + \frac{6}{256} = \frac{43}{128}
\end{align*} \]
으로 동일한 결과를 얻는다.$ $
$ $
다음과 같은 형태의 무한급수
\[ \sum_{n=0}^{\infty} \frac{n}{2^n}, \quad \sum_{n=1}^{\infty} \frac{2n+1}{2^{n}}, \quad \sum_{n=1}^{\infty} \frac{n^2-4}{2^{n+1}}, \quad \sum_{n=0}^{\infty} \frac{n^2+n+1}{2^{n+1}} \]
의 값은 모두 정수이다. (실제로 계산해 보면, 각각 $2,\, 5,\, 1,\, 5$가 나옴을 확인할 수 있다.) 이러한 사실은 성립한다는 사실은 위 정리로부터 쉽게 알 수 있는데, 이는 다음 따름정리에서 확인해 보자.
$ $
따름정리. $p(x)$가 $d$차 정수계수 다항함수라 하자. 그러면 다음 무한급수
\[ \sum_{n=0}^{\infty} \frac{p(n)}{2^{n+1}} \]
의 합은 언제나 정수이다.
$ $
증명. 위 정리에서 $a=2$인 경우이므로,
\[ \sum_{n=0}^{\infty} \frac{p(n)}{2^{n+1}} = \sum_{k=0}^{d} \frac{\Delta(k,\, 0)}{(2-1)^{k+1}} = \sum_{k=0}^{d} \Delta(k,\, 0) \]
$p(x)$가 정수계수만을 가지므로, 모든 $n$에 대하여 $p(n)$ 또한 정수이고, 따라서 $\Delta(k,\, 0)$ 또한 정수임을 알 수 있다. 즉, 위 식의 우변은 정수 $\Delta(k,\, 0)$들의 유한합이므로 정수가 된다.$ $
$ $