연이은 $2n+1$개의 자연수의 제곱의 합

      Comments Off on 연이은 $2n+1$개의 자연수의 제곱의 합

연이은 세 양의 정수 $3,\,4,\,5$ 사이에는 우리에게 잘 알려진 피타고라스 정리(Pythagorean theorem)가 성립한다.

\[ 3^2 + 4^2 = 5^2 \]

나아가 연이은 다섯개의 양의 정수 $10,\, \ldots,\,14$와 연이은 일곱개의 양의 정수 $21,\, \ldots,\, 27$ 사이에도 위와 비슷한 관계가 성립함을 알 수 있다.

\[ \begin{align*} 3^2 + 4^2 &= 5^2 \\[5px] 10^2 + 11^2 + 12^2 &= 13^2 + 14^2 \\[5px] 21^2 + 22^2 + 23^2 + 24^2 &= 25^2 + 26^2 + 27^2 \end{align*} \]

일반적으로 음이 아닌 정수 $n$에 대하여, 연이은 $2n+1$개의 양의 정수 $x-n,\, \ldots,\, x+n$을 잘 택하여 처음 $n+1$개의 양의 정수의 제곱의 합이 나중 $n$개의 양의 정수의 제곱의 합과 같아지도록 할 수 있다. 다시 말해 아래의 식

\[ (x-n)^2 + \cdots + (x-1)^2 + x^2 = (x+1)^2 + \cdots + (x+n)^2 \tag*{$\myblue{(\ast)}$} \]

을 만족하는 ($n$보다 큰) 양의 정수 $x$가 언제나 존재한다. 또한 이 조건을 만족하는 양의 정수 $x$는 각각의 $n \in \N$에 대하여 유일하게 존재한다.

$ $

정리.

임의의 양의 정수 $n \in \N$에 대하여

\[ T_n = \sum_{k=1}^{n} k = 1 + 2 + \cdots + n \]

이라 정의하자. (이 $T_n$을 $n$번째 삼각수(triangle number)라 부른다.) 그러면 $2n+1$개의 연이은 양의 정수들에 대한 등식 $\myblue{(\ast)}$를 만족하는 해는 $x = 4T_n$이 유일하다. 즉, 오직 $x=4T_n$에 대하여 다음 등식이 성립한다.

\[ (4T_n - n)^2 + \cdots + (4T_n - 1)^2 + (4T_n)^2 = (4T_n + 1)^2 + \cdots + (4T_n + n)^2 \]

$ $

증명. 양의 정수 $n \in \N$을 고정하자. 먼저 임의의 두 양의 정수 $x,\, k \in \N$에 대하여 다음 등식이 성립한다.

\[ (x-k)^2 + 4kx = (x+k)^2 \]

이제 위 등식에 $k=1,\,2,\, \ldots,\, n$을 대입한 뒤 모두 더해주면,

\[ (x-n)^2 + \cdots + (x-1)^2 + 4T_nx = (x+1)^2 + \cdots + (x+n)^2  \]

를 얻는다. 위 식을 $\myblue{(\ast)}$와 비교하면 $x^2 = 4T_nx$이어야 하므로 $x=0$ 또는 $x=4T_n$을 얻는다. 이 중 $x=0$은 조건을 만족하지 않으므로, $\myblue{(\ast)}$를 만족하는 유일한 해는 $x=4T_n$임을 알 수 있다..

$ $

$4T_n = 2n(n+1) = 2n^2 + 2n$이므로 $\myblue{(\ast)}$를 만족하는 유일한 양의 정수 해는 $2n^2 + n$ 부터 $2n^2 + 3n$ 까지의 $2n+1$개의 양의 정수임을 알 수 있다.

$ $

수학 저널 Mathematics Magazine에 2000년에 실린 글 [Michael Boardman, Mathematics Magazine, Vol. 73, No. 1 (Feb., 2000), p. 59]에는 위 정리에서 $n=3$인 경우에 대한 말없는 증명(proof without words)가 실려있다.

$ $

$ $

삼각수(triangle number)와의 관계

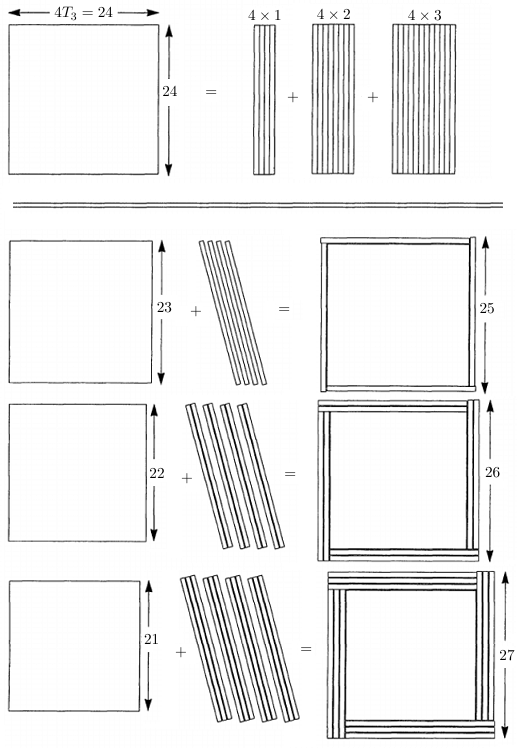
삼각수(triangle number) $T_n$는 $n$이하의 모든 양의 정수의 합을 나타낸는 수로써 $T_n = \frac{1}{2}n(n+1)$과 같이 주어진다. 첫 몇 개의 삼각수를 나타내면 다음과 같다. (OEIS: A000217)

\[ 0,\, 1,\, 3,\, 6,\, 10,\, 15,\, 21,\, 28,\, 36,\, 45,\, 55,\, \ldots \]

우리가 이전에 구했던 식 $\myblue{(\ast)}$을 만족하는 연이은 $2n+1$개의 양의 정수쌍의 제일 처음 수를 나열해 보면, (OEIS: A014105)

\[ 0,\, 3,\, 10,\, 21,\, 36,\, 55,\, 78,\, 105,\, 136,\, 171,\, 210\, \ldots \]

이다. 위 수열의 일반항은 (위에서 구했듯이) $2n^2 + n = n(2n+1)$이고 이는 $T_{2n}$와 같음을 알 수 있다. 또한 식 $\myblue{(\ast)}$을 만족하는 연이은 $2n+1$개의 양의 정수쌍의 가운데 수는 $4T_n$이었고, 이 수열을 나열해 보면, (OEIS: A046092)

\[ 0,\, 4,\, 12,\, 24,\, 40,\, 60,\, 84,\, 112,\, 144,\, 180,\, 220,\, \ldots \]

이다. 마지막으로 식 $\myblue{(\ast)}$을 만족하는 연이은 $2n+1$개의 양의 정수쌍의 제일 마지막 수를 나열해 보면, (OEIS: A014106)

\[ 0,\, 5,\, 14,\, 27,\, 44,\, 65,\, 90,\, 119,\, 152,\, 189,\, 230,\, \ldots \]

이고, 위 수열의 일반항은 $2n^2 + 3n = n(2n+3)$이고, 간단한 계산을 통해 $T_{2n+1} - 1$의 값과 같음을 확인해 볼 수 있다.

$ $