$ $
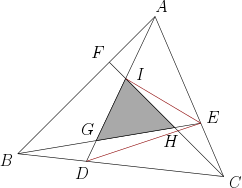
풀이. 먼저 아래와 같이 보조선 $DE$와 $IE$를 그린다.

$ $

$ $
그러면 삼각형 $IGH$와 삼각형 $ABC$의 넓이의 비는 아래의 식을 통해서 구할 수 있다.
\[ \frac{\triangle IGH}{\triangle ABC} = \frac{\triangle ADC}{\triangle ABC}
\cdot \frac{\triangle ADE}{\triangle ADC} \cdot \frac{\triangle
IGE}{\triangle ADE} \cdot \frac{\triangle IGH}{\triangle IGE} \]
이 중,
\[ \begin{align*} \frac{\triangle ADC}{\triangle ABC} &= \frac{DC}{BC} = \frac{2}{3},
& \frac{\triangle ADE}{\triangle ADC} &= \frac{AE}{AC} = \frac{2}{3}, \\[5px] \frac{\triangle IGE}{\triangle ADE} &= \frac{IG}{AD}, & \frac{\triangle IGH}{\triangle IGE} &= \frac{GH}{GE} \end{align*} \]
이므로 결국
\[ \frac{\triangle IGH}{\triangle ABC} = \frac{4}{9} \cdot
\frac{IG}{AD} \cdot \frac{GH}{GE} \]
를 통해 삼각형 $IGH$와 삼각형 $ABC$의 넓이의 비를 구할 수 있다.
$ $
이제 삼각형 $ABD$와 선분 $FC$에 메넬리우스의 정리(Menelaus' Theorem)을 적용하면
\[ -1 = \frac{AF}{FB} \cdot \frac{BC}{CD} \cdot \frac{DI}{IA} = \frac{1}{2}
\cdot \left( -\frac{3}{2} \right) \cdot \frac{DI}{IA} \]
따라서 $DI : IA = 4:3$을 얻는다. 또한 삼각형 $ADC$와 선분 $BE$에 메넬리우스의 정리를 적용하면
\[ -1 = \frac{AG}{BD} \cdot \frac{DB}{BC} \cdot \frac{CE}{EA} =
\frac{AG}{GD} \cdot \left( -\frac{1}{3} \right) \cdot \frac{1}{2} \]
그러므로 $AG : GD = 6 : 1$을 얻는다.
$ $
$ $
따라서
\[ \frac{IG}{AD} = \frac{AG}{AD} - \frac{AI}{AD} = \frac{6}{7} -
\frac{3}{7} = \frac{3}{7} \]
을 얻는다. 나아가 $GH : GE = IG : ID$라는 사실을 이용하면
\[ \frac{GH}{GE} = \frac{IG}{ID} = \frac{IG}{AD} \cdot \frac{AD}{ID} =
\frac{3}{7} \cdot \frac{7}{4} = \frac{3}{4} \]
이제 이 사실들을 모두 종합하면 최종적으로 삼각형 $IGH$와 삼각형 $ABC$의 넓이의 비는
\[ \frac{\triangle IGH}{\triangle ABC} = \frac{4}{9} \cdot
\frac{IG}{AD} \cdot \frac{GH}{GE} = \frac{4}{9} \cdot \frac{3}{7} \cdot
\frac{3}{4} = \frac{1}{7} \]
즉, 삼각형 $IGH$의 넓이는 언제나 삼각형 $ABC$의 넓이의 $1/7$이 됨을 알 수 있다..