브레치나이더 공식(Bretschneider's formula)은 임의의 사각형의 네 변의 길이와 마주보는 두 각의 크기를 이용하여 사각형의 넓이를 계산하는 공식을 뜻한다. 이 공식은 원에 내접한 사각형의 넓이를 구하는 브라마굽타 공식(Brahmagupta's formula)과 삼각형의 넓이를 구하는 헤론의 공식(Heron's formula)의 확장으로 볼 수 있다.
$ $
$ $
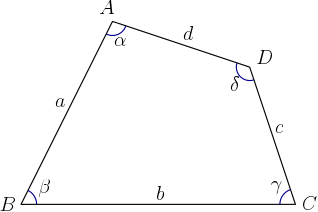
증명. 다음과 같이 사각형 $ABCD$가 주어졌다고 하자.
사각형 $ABCD$의 넓이는 삼각형 $ABD$와 삼각형 $BCD$의 넓이의 합과 같으므로
\[ K = \frac{ad\sin(\alpha)}{2} + \frac{bc\sin(\gamma)}{2} \]
로 나타낼 수 있다. 이제 위 식의 양변을 제곱하고 $16$을 곱해주어 정리하면,
\[ 16K^2 = 4(ad)^{2}\sin^{2}(\alpha) + 4(bc)^{2}\sin^{2}(\gamma) + 8abcd\sin(\alpha)\sin(\gamma) \tag*{$\myblue{(1)}$} \]
를 얻는다. 한 편, 제 2 코사인 법칙에 의해서
\[ a^{2} + d^{2} - 2ad\cos(\alpha) = b^{2} + c^{2} - 2bc\cos(\gamma) \]
이다. 이제 위 식을 정리한 후에 양변을 제곱하여 정리하면,
\[ (a^{2} + d^{2} - b^{2} - c^{2})^2 = 4(ad)^{2}\cos^{2}(\alpha) + 4(bc)^{2}\cos^{2}(\gamma) - 8abcd \cos(\alpha)\cos(\gamma) \tag*{$\myblue{(2)}$} \]
를 얻는다. 다음으로 식 $\myblue{(1)}$과 $\myblue{(2)}$를 더해준 후에 삼각함수의 반각공식을 이용하여 정리하면,
\[ \begin{align*}
16K^{2} + (a^{2} + d^{2} & - b^{2} - c^{2})^{2} \\[5px]
&= 4(ad)^{2} + 4(bc)^{2} - 8abcd\cos(\alpha +\gamma) \\[5px]
&= 4(ad + bc)^{2} - 8abcd - 8abcd\cos(\alpha +\gamma) \\[5px]
&= 4(ad + bc)^{2} - 8abcd \Big[ \cos(\alpha +\gamma) + 1 \Big] \\[5px]
&= 4(ad + bc)^{2} - 16abcd\cos^{2}\left( \tfrac{\alpha + \gamma}{2} \right) \tag*{$\myblue{(3)}$}
\end{align*} \]
를 얻는다. 위 식 $\myblue{(3)}$을 정리하기 위해 먼저 $s=\tfrac{a+b+c+d}{2}$를 이용하여 다음의 식을 정리하자.
\[ \begin{align*}
4(ad + bc)^{2} &- (a^{2} + d^{2} - b^{2} - c^{2})^2 \\[5px]
&= \Big[ 2(ad + bc) + (a^{2} + d^{2} - b^{2} - c^{2}) \Big] \Big[ 2(ad + bc) - (a^{2} + d^{2} - b^{2} - c^{2}) \Big] \\[5px]
&= \Big[ (a+d)^{2} - (b-c)^2 \Big] \Big[ (b+c)^{2} - (a-d)^2 \Big] \\[5px]
&= (a + d + b - c)(a + d - b + c)(b + c + a - d)(b + c - a + d) \\[5px]
&= (2s - 2c)(2s - 2b)(2s - 2d)(2s - 2a) \tag*{$\myblue{(4)}$}
\end{align*} \]
마지막으로 식 $\myblue{(4)}$를 식 $\myblue{(3)}$에 대입하면,
\[ 16K^{2} = (2s - 2c)(2s - 2b)(2s - 2d)(2s - 2a) - 16abcd\cos^{2}\left( \tfrac{\alpha + \gamma}{2} \right) \]
을 얻을 수 있고, 위 식의 양변을 $16$으로 나눈 뒤 제곱근을 취해주면 우리가 원하는 공식을 얻는다..<\span>
$ $
참고. 사각형 $ABCD$에서 마주보는 두 각은 어떤 것을 택하든지 상관이 없다. 왜냐하면 $\beta + \delta = 2\pi - (\alpha + \gamma)$가 성립하므로
\[ \cos^{2} \left( \tfrac{\beta + \delta}{2} \right) = \cos^{2} \left( \tfrac{2\pi - (\alpha + \gamma)}{2} \right) = \cos^{2} \left( \pi - \tfrac{\alpha + \gamma}{2} \right) = \cos^{2} \left( \tfrac{\alpha + \gamma}{2} \right) \]
이기 때문이다.
$ $
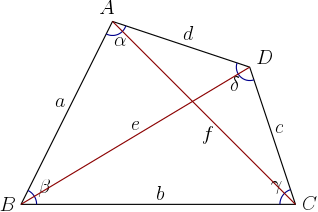
참고. 브레치나이더 공식을 변형하면, 사각형 $ABCD$의 네 변의 길이 $a,\, b,\, c,\,d$와 두 대각선의 길이 $e,\, f$를 이용하여 사각형의 넓이를 구하는 것이 가능하다.
\[ \begin{align*}
K &= \sqrt{(s-a)(s-b)(s-c)(s-d) - \tfrac{1}{4}(ac + bd + ef)(ac + bd - ef)} \\[5px]
&= \frac{1}{4} \sqrt{4e^2f^2 - (a^2 - b^2 + c^2 - d^2)^2}
\end{align*} \]
$ $
$ $
증명. 원에 내접하는 사각형의 마주보는 두 각의 합은 언제나 $\pi$이므로 브레치나이더 공식에서 $\cos(\tfrac{\alpha + \gamma}{2}) = \cos(\tfrac{\pi}{2}) = 0$이 되어 브라마굽타 공식을 얻는다..
$ $
$ $
증명. 원에 외접하는 사각형에 대하여 $a+c = b+d = s$가 성립하므로, 이를 브레치나이더 공식에 대입하여 정리하면 원하는 결과를 얻는다..
$ $
$ $
증명. 브라마굽타 공식에서 $d \to 0$의 극한을 취해주면 헤론의 공식을 얻는다..