삼각함수(trigonometric function)와 쌍곡함수(hyperbolic function)는 서로 밀접한 관계가 있는데, 이는 복소수를 이용하여 다음과 같이 나타낼 수 있다.
\[ \begin{align*}
\sin(iz) &= i\sinh(z) & \sinh(iz) &= i\sin(z) \\[5px]
\cos(iz) &= \cosh(z) & \cosh(iz) &= \cos(z) \\[5px]
\tan(iz) &= i\tanh(z) & \tanh(iz) &= i\tan(z) \\[5px]
\cot(iz) &= -i\coth(z) & \coth(iz) &= -i\cot(z) \\[5px]
\sec(iz) &= \sech(z) & \sech(iz) &= \sec(z) \\[5px]
\csc(iz) &= -i\csch(z) & \csch(iz) &= -i\csc(z)
\end{align*} \]
하지만 구데르만 함수를 이용하면, 굳이 복소수를 이용하지 않아도 삼각함수와 쌍곡함수의 밀접한 관련성을 확인할 수 있다.
$ $
구데르만 함수(Gudermannian function)
구데르만 함수(Gudermannian function) $\operatorname{gd} : \R \to \R$는 다음과 같이 $\sech(x)$의 적분으로 정의되는 함수이다.
\[ \operatorname{gd}(x) = \int_{0}^{x} \sech(t) \,dt \tag*{$(\ast)$}\]
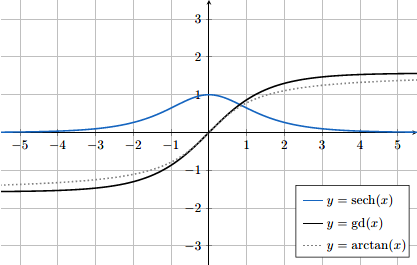
특히 미적분학의 기본정리(funcdamental theorem of Calculus)에 의해 $\operatorname{gd}'(x) = \sech(x)$를 얻는다. 아래 그래프는 $y = \sech(x)$와 $y = \operatorname{gd}(x)$의 그래프를 각각 나타낸 것이다. 비교를 위해 $y = \arctan(x)$의 그래프도 같이 나타내었다.
한 편, 식 $(\ast)$의 우변을 $u = \sinh(t)$, $du = \cosh(t) dt$를 이용하여 치환적분을 하면
\[ \begin{align*}
\operatorname{gd}(x) &= \int_{0}^{x} \sech(t) \,dt = \int_{0}^{x} \frac{\cosh(t)}{\cosh^2(t)} \,dt = \int_{0}^{x} \frac{\cosh(t)}{1 + \sinh^2(t)} \,dt \\[5px]
&= \int_{0}^{\sinh(x)} \frac{1}{1 + u^2} \,du = \arctan(u) \, \Big|_{0}^{\sinh(x)} = \arctan(\sinh(x))
\end{align*} \]
따라서 $\tan(\operatorname{gd}(x)) = \sinh(x)$를 얻는다.
$ $
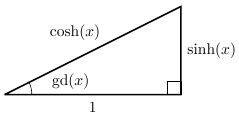
즉, 밑변의 길이가 $1$이고 높이가 $\sinh(x)$인 삼각형의 한 각의 크기가 $\operatorname{gd}(x)$이므로 다음 그림과 같은 삼각형을 얻는다.
위 삼각형을 이용하여 삼각함수와 쌍곡함수의 관계에 대한 항등식을 더 얻을 수 있다.
\[ \begin{align*}
\sin(\operatorname{gd}(x)) &= \tanh(x) & \csc(\operatorname{gd}(x)) &= \coth(x) \\[5px]
\cos(\operatorname{gd}(x)) &= \sech(x) & \sec(\operatorname{gd}(x)) &= \cosh(x) \\[5px]
\tan(\operatorname{gd}(x)) &= \sinh(x) & \cot(\operatorname{gd}(x)) &= \csch(x)
\end{align*} \]
$ $
역 구데르만 함수(inverse Gudermannian function)
구데르만 함수는 일대일 함수이므로 구간 $(-\frac{\pi}{2},\, \frac{\pi}{2})$ 위에서 역함수가 존재한다. 이 함수를 $\operatorname{igd}$라 하자. $\operatorname{gd}'(x) = \sech(x)$이므로 역함수의 미분법에 의해
\[ \operatorname{igd}'(x) = \frac{1}{\operatorname{gd}'(y)} = \frac{1}{\sech(y)} = \cosh(y) = \sec(\operatorname{gd}(y)) = \sec(x) \]
또한 $\operatorname{igd}(0) = 0$이므로, 미적분학의 기본정리에 의해
\[ \operatorname{igd}(x) = \int_{0}^{x} \sec(t) \,dt = \ln(\sec(x) + \tan(x)) \]
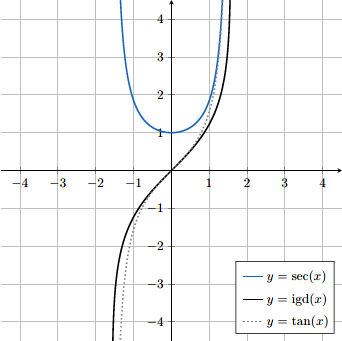
와 같이 나타낼 수 있다. $y = \sec(x)$와 $y = \operatorname{igd}(x)$의 그래프는 각각 다음과 같다. 역시 비교를 위해 $y = \tan(x)$의 그래프도 같이 나타내었다.
역 구데르만 함수를 이용하면 삼각함수와 쌍곡함수 사이에 아래와 같은 관계가 있음을 알 수 있다.
\[ \begin{align*}
\sinh(\operatorname{igd}(x)) &= \tan(x) & \csch(\operatorname{igd}(x)) &= \cot(x) \\[5px]
\cosh(\operatorname{igd}(x)) &= \sec(x) & \sech(\operatorname{igd}(x)) &= \cos(x) \\[5px]
\tanh(\operatorname{igd}(x)) &= \sin(x) & \coth(\operatorname{igd}(x)) &= \csc(x)
\end{align*} \]