삼각수(triangular number)란 어떠한 물체를 삼각형 모양으로 쌓았을 때, 그 삼각형을 만들기 위해서 필요한 물체의 총 개수가 되는 수를 말한다. 아래 그림은 첫 다섯개의 삼각수들을 보여준다.
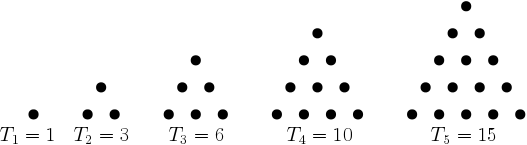
비슷한 방법으로 사각수(square number)를 어떠한 물체를 사각형 모양으로 쌓았을 때, 그 사각형을 만들기 위해서 필요한 물체의 총 개수가 되는 수로 정의하자. 아래 그림은 첫 다섯개의 사각수들을 보여준다.
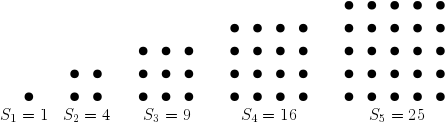
간단한 계산을 통해 $k$번 째 삼각수 $T_k$와 사각수 $S_k$는 아래의 식을 통해 구할 수 있음을 알 수 있다.
\[ T_k = \frac{k(k+1)}{2}, \qquad S_k = k^2. \]
또한 $1$은 첫번째 삼각수이면서, 동시에 첫번째 사각수가 된다. 이러한 숫자를 사각삼각수(square triangular number)라 정의하자. 또다른 사각삼각수는 $36$이다. 왜냐하면,
\[ 36 = \frac{8(8+1)}{2} = 6^2. \]
즉, $36$은 여덟번째 삼각수이면서, 동시에 여섯번째 사각수가 되기 떄문이다. 그렇다면 $1$과 $36$을 제외한 또 다른 사각삼각수가 존재할까? 만약 사각삼각수의 개수가 유한하다면 가장 큰 사각삼각수는 무엇일까? 반대로 사각삼각수의 개수가 무한하다면, 사각삼각수를 생성하는 공식 같은 것이 존재할까?
먼저 사각삼각수를 수학적으로 다시한번 정의해보자.
이렇게 정의된 사각삼각수 $N_k$의 개수는 무한하고 아래와 같은 방법으로 $N_k$를 계산할 수 있다.
증명. 먼저 아래의 계산을 살펴보자.
따라서 $t_k$가 양의 정수가 되기 위해서 (따라서 $N_k$가 사각삼각수가 되기 위해서) 반드시 $1+8s_k^2$가 완전제곱수가 되어야만 함을 알 수 있다. 즉, 적당한 양의 정수 $r_k$가 존재하여
을 만족해야 한다. 위와 같은 형태의 방정식을 펠방정식(Pell's equation)이라 하는데, 이 펠방정식의 해는 다음과 같은 방법으로 구할 수 있음이 알려져 있다: 우선 $(r_0,\, s_0) = (1,\,0)$은 위 펠방정식을 만족하는데 이를 자명해(trivial solution)이라 한다. 그리고 자명해가 아닌 최소의 해를 기본해(fundamental solution)라 하고 이를 $(r_1,\, s_1)$로 나타내면, 점화식
을 통해 일반해 $(r_k,\, s_k)$를 구할 수 있다. 또한 이 펠방정식의 기본해 $(r_1,\, s_1)$ 또한 $\sqrt{8} = 2\sqrt{2}$의 연분수(continued fraction) 계산을 통해서 구할 수 있음이 알려져 있다. (나중에 기회가 되면 자세히 다뤄보도록 하자.) 이 방법을 통해 $(r_1,\, s_1) = (3,\,1)$를 구할 수 있고, 점화식을 이용하여 일반해 $(r_k,\, s_k)$를 구할 수 있다. 마지막으로 아래의 대입
을 이용하여, $k$번째 사각삼각수 $N_k$와 $s_k$, $t_k$를 모두 구할 수 있다.
먼저 첫 두개의 사각삼각수의 값을 직접 계산해 보자. 우선 $(r_1,\, s_1) = (3,\,1)$이므로 이를 이용하면,
을 얻는다. 이제 두번째 사각삼각수의 값을 구하기 위해 $(r_2,\,s_2)$의 값을 구해보자.
따라서 $(r_2,\,s_2) = (17,\,6)$을 얻고 이를 이용하여,
을 얻는다.
$k = 0,\, \ldots,\ 10$일 때, 사각삼각수 $N_k$와 각각에 대응하는 $r_k$, $s_k$, $t_k$를 표로 나타내면 아래와 같다.
| $k$ | $r_k$ | $s_k$ | $t_k$ | $N_k$ |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 1 | 3 | 1 | 1 | 1 |
| 2 | 17 | 6 | 8 | 36 |
| 3 | 99 | 35 | 49 | 1225 |
| 4 | 577 | 204 | 288 | 41616 |
| 5 | 3363 | 1189 | 1681 | 1413721 |
| 6 | 19601 | 6930 | 9800 | 48024900 |
| 7 | 114243 | 40391 | 57121 | 1631432881 |
| 8 | 665857 | 235416 | 332928 | 55420693056 |
| 9 | 3880899 | 132105 | 1940449 | 1882672131025 |
| 10 | 22619537 | 7997214 | 11309768 | 63955431761796 |