$1$부터 $6$까지의 숫자가 각 면에 적혀있는 일반적인 정육면체 모양 주사위 두 개 $A$와 $B$가 주어졌다고 하자. 이제 주사위 $A$가 주사위 $B$를 이길 확률, 질 확률, 비길 확률 (즉, 주사위 $A$와 $B$를 던졌을 때, $A$의 눈이 $B$의 눈보다 클 확률, 작을 확률, 같을 확률)을 각각 $P(A > B)$, $P(A < B)$, $P(A = B)$로 정의하면 간단한 계산을 통해
임을 알 수 있다. 즉, 두 주사위 $A$와 $B$에 대하여, 한 주사위가 다른 주사위를 이길 확률은 각각 $\frac{15}{36}$으로 동일하다. 이와 같이 두 주사위 $A$와 $B$에 대하여 $P(A > B) = P(A < B)$가 성립하는 경우 기호로 $A \simeq B$로 나타내기로 하자.
$ $
이번에는 모든 면에 $6$이 적혀 있는 정육면체 모양 주사위 $A$와 모든 면에 $1$이 적혀 있는 정육면체 모양 주사위 $B$를 생각해 보자. 그러면 주사위 $A$가 항상 주사위 $B$를 이기게 된다. (즉, $P(A > B) = 1 > 0 = P(A < B)$가 성립한다.) 이와 같이 두 주사위 $A$와 $B$에 대하여 $P(A > B) > P(A < B)$가 성립하는 경우 기호로 $A \succeq B$로 나타내기로 하자.
$ $
각 면에 양의 정수가 적혀 있는 $n \geq 3$개의 정육면체 모양 주사위의 집합 $\{A_1,\, A_2,\, \ldots,\, A_n\}$이 주어졌다고 하자. 각각의 주사위에 대하여 다음과 같은 관계
이 성립할 때, 주사위의 집합 $\{A_1,\, A_2,\, \ldots,\, A_n\}$은 반추이적(nontransitive)이라 한다. "가위-바위-보 게임"은 반추이적 성질을 가지는 가장 간단하면서 유명한 게임이다.
$ $
$n=3$인 경우, 다음과 같은 예가 있다.
각각의 경우에 대하여 경우의 수를 생각해 보면
가 되어 $A_1 \succeq A_2 \succeq A_3 \succeq A_1$, $B_1 \succeq B_2 \succeq B_3 \succeq B_1$이 성립한다. 즉 두 주사위 집합 모두 반추이적임을 알 수 있다.
$ $
하지만 두 주사위 집합 $\{A_1,\, A_2,\, A_3\}$, $\{B_1,\, B_2,\, B_3\}$은 다음과 같은 흥미로운 차이점을 갖는다. 이를 알아보기 위하여, 각 집합의 세 주사위가 동시에 던지는 경우를 생각해 보자. 먼저 주사위 집합 $\{A_1,\, A_2,\, A_3\}$의 세 주사위를 동시에 던질 때, 각 주사위가 다른 두 주사위를 동시에 이길 확률을 계산하면 각각
가 되어 $A_2$가 게임에서 가장 불리함을 알 수 있다. 반면 주사위 집합 $\{B_1,\, B_2,\, B_3\}$에 대하여도 같은 계산을 해 보면
이 되어 이번에는 반대로 $B_2$가 가장 유리한 주사위가 된다. 따라서 두 주사위 집합은 모두 반추이적이기는 하지만 서로 동형은 아님을 알 수 있다.
$ $
1975년 물리학자 마이클 윈켈만(Michael Winkelmann)은 다음과 같은 형태의 반추이적 주사위를 제안하였다.
위 주사위 역시 한 주사위가 다른 주사위를 이길 확률을 각각 계산해 보면
이 되어 반추이적 성질 $M_1 \succeq M_2 \succeq M_3 \succeq M_1$, $N_1 \succeq N_2 \succeq N_3 \succeq N_1$을 가짐을 확인해 볼 수 있다. 이 주사위를 마이윈 주사위(Miwin dice)라 부른다.1
$ $
마이윈 주사위 집합 $\{M_1,\, M_2,\, M_3\}$ 또는 $\{N_1,\, N_2,\, N_3\}$에 적힌 주사위들의 눈을 살펴보면 $1$부터 $9$ 까지의 숫자가 정확히 두 번씩 사용되었음을 알 수 있다. 이 사실을 이용하여 $0 \sim 80$의 숫자 중 하나를 뽑는 시행이 균등분포(uniform distribution)을 갖도록 설계할 수 있다. 다음과 같은 시행을 살펴보자.
- 첫번째 마이윈 주사위 집합 $\{M_1,\, M_2,\, M_3\}$에서 하나의 주사위를 무작위로 선택하여 던진다. 이 때 나온 주사위의 눈을 $a$라 하자.
- 두번째 마이윈 주사위 집합 $\{N_1,\, N_2,\, N_3\}$에서 하나의 주사위를 무작위로 선택하여 던진다. 이 때 나온 주사위의 눈을 $b$라 하자.
- $N := 9a - b$의 값을 계산한다. 이 때, $N$은 $0$부터 $80$ 사이의 정수 값을 갖는다.
위 시행에서 계산한 $N$의 값의 분포는 균등분포를 갖는다. 실제로 임의의 정수 $0 \leq k \leq 80$에 대하여, $P(N = k) = \frac{1}{81}$임을 간단히 확인할 수 있다.
$ $
독일의 퍼즐 제작자 오스카 반 데벤터(Oskar van Deventer)2는 다음과 같이 7개의 반추이적 주사위를 제안하였다.
실제로 확률 계산을 통해 $O_1$은 $\{O_2,\, O_3,\, O_5\}$를 이기고, $O_2$는 $\{O_3,\, O_4,\, O_6\}$를 이기고, $O_3$는 $\{O_4,\, O_5,\, O_7\}$을 이기고, $O_4$는 $\{O_5,\, O_6,\, O_1\}$을 이기고, $O_5$는 $\{O_6,\, O_7,\, O_2\}$를 이기고, $O_6$는 $\{O_7,\, O_1,\, O_3\}$를 이기고, 마지막으로 $O_7$은 $\{O_1,\, O_2,\, O_4\}$를 이김을 확인할 수 있다. 이를 방향그래프(digraph)로 나타내면 다음과 같다. 여기서 $A \to B$는 $A$가 $B$를 이김을 뜻한다.
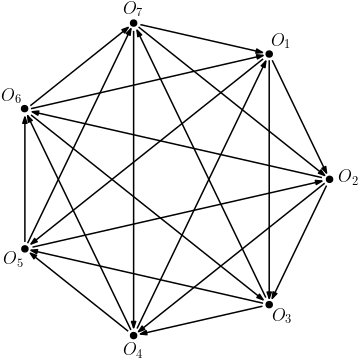
또한 오스카 주사위 집합 $\{O_1,\, \ldots,\, O_7\}$에서 임의로 두개의 주사위를 고르면, 이 주사위들을 모두 이기는 오스카 주사위가 유일하게 존재한다. 예를 들어 $\{O_3,\, O_7\}$은 모두 이기는 주사위는 $O_6$임을 알 수 있다.
$ $
$ $