평면상의 직선이란 직관적으로 무한이 길고 곧은 선을 의미한다. 이 평면상의 직선 등을 다루는 기하학이 바로 평면기하학, 유클리드 기하학 등으로 불린다. 그렇다면 구면상에서의 직선은 어떻게 정의할 수 있을까? 구면상에서의 직선은 바로 구면상에 있는 대원(great circle)이 된다. 구면 위에 두 점이 있을 때, 그 두 점과 구의 중심은 하나의 평면을 결정하고, 그 평면과 구면이 만나서 그리는 원을 대원이라고 한다. 구면위의 두 점을 잇는 선분 또한 같은 방법으로 얻을 수 있다. (두 점을 지나는 대원을 구하면, 이 두점이 대원을 두 부분으로 나누게 되는데 이 중 짧은 쪽을 두 점을 잇는 선분으로 정의한다.)
이제 구면위에 세 점이 있을 때 이 세 점을 이어 만들어진 구면삼각형(spherical triangle) $ABC$를 생각해 보자.
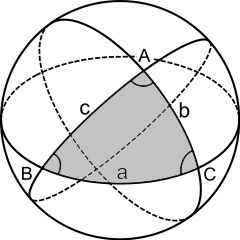
이와 같은 삼각형 $ABC$의 넓이를 어떻게 구할수 있을까? 이를 위해서는 먼저 몇 가지 사실들을 살펴 보아야 한다.
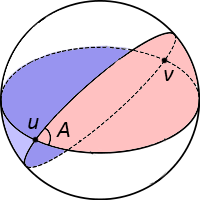
- 먼저 구면 위에 두 대원의 교점들은 항상 대척점(antipodal point)이 됨을 알 수 있다. 즉, 위 그림에서 점 $u$와 $v$는 원점을 중심으로 서로 반대방향에 놓여 있다.
- 만약 두 대원 사이의 각도가 $A$로 주어졌다면, 이 대원들이 만나서 생기는 초승달 모양의 넓이는 $2Ar^2$이 된다. 이는 넓이가 각도에 비례한다는 사실과, 구면의 넓이는 $4\pi r^2$이라는 사실을 이용하면 된다.
- 마지막으로 서로 마주보는 초승달 모양의 영역의 넓이는 같음을 알 수 있다. 즉, 위 그림에서 붉은 영역과 파란 영역의 넓이는 서로 갖다.
이제 이 사실들을 이용해서 세 각이 각각 $A,\, B,\, C$로 주어진 구면삼각형의 넓이를 구해보자.
증명. 먼저 구면삼각형의 넓이를 $\Delta$라 정의하자.
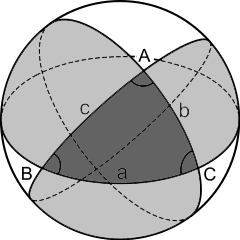
위의 그림처럼, 구면삼각형의 각 선분을 연장하여 반대편 극에 마주보고 있는 점까지 대원을 잇는다. 그러면 위에처럼 회색으로 칠한 초승달 모양의 영역 세개를 얻을 수 있다. 그러면 위에서 관찰한 (3)에 의하여 이 회색으로 칠한 영역은 정확히 구면의 넓이의 절반임을 알 수 있다. 또한 초승달 모양의 영역의 넓이는 (2)에서 관찰한 바와 같이 각각 $2Ar^2,\, 2Br^2,\, 2Cr^2$임을 알 수 있다. 각각의 초승달 모양 영역은 구면삼각형을 포함하므로, 초승달 모양 영역의 넓이의 합에는 구면삼각형의 넓이가 총 3번 반복되게 된다. 따라서 이 사실들을 모두 종합하면,
그러므로 위 식을 정리하면 구면삼각형의 넓이 $\Delta = r^2(A+B+C - \pi)$를 얻게 된다..
위와 같은 사실은 Girard의 정리라 불린다.
또한 위 정리의 따름 정리로써 아래와 같은 놀라운 사실을 얻을 수 있다: 즉, 구면 위의 구면삼각형의 세 각의 합은 언제나 180도보다 크다!
증명. Girard의 공식을 정리하면,
를 얻는다. 이때 구면삼각형의 넓이는 언제나 양수이므로 원하는 부등식이 성립한다..