원이 하나 주어졌다고 하자. 이 원에 외접하는 정삼각형을 하나 그리고 다시 정삼각형에 외접하는 원을 그린다. 이제 이 원에 외접하는 정사각형을 그리고 다시 정사각형에 외접하는 원을 그린다. 다음으로 이 원에 외접하는 정오각형을 그리고 다시 정오각형에 외접하는 원을 그린다. 이와 같은 행위를 계속 반복하면 반지름이 점점 커지는 무한히 많은 동심원들이 그려지게 될 것이다. 이 때, 가장 바깥쪽에 그려지게 될 원은 무한히 커지게 될까?

$ $

이번에는 반대로 생각해 보자. 주어진 원에 대하여, 원에 내접하는 정삼각형을 하나 그리고 다시 정삼각형에 내접하는 원을 그린다. 이제 이 원에 내접하는 정사각형을 그리고 다시 정사각형에 내접하는 원을 그린다. 다음으로 이 원에 내접하는 정오각형을 그리고 다시 정오각형에 내접하는 원을 그린다. 이와 같은 행위를 계속 반복하면 반지름이 점점 작아지는 무한히 많은 동심원들이 그려지게 될 것이다. 이 때, 가장 안쪽에 그려지게 될 원은 점으로 수렴하게 될까?

$ $

먼저 첫번째 문제에 대해 생각해 보자. 아래 그림은 제일 안쪽의 작은 원에서 시작해서 정 $24$각형에 외접하는 원까지를 그린 그림이다.

$ $

$ $

위 그림을 보면 가장 바깥쪽에 그려지게 될 원의 반지름이 어떤 특정한 값으로 수렴할 것이라 짐작해 볼 수 있다. 이제 이 사실을 수학적으로 증명해 보자.

$ $

주어진 정 $n$각형의 한 변의 길이를 $s_n$이라 하자. 그러면 정 $n$각형의 내접원과 외접원의 반지름의 길이 $r_n$과 $R_n$은 각각 다음의 공식을 이용해 구할 수 있다. \[ r_n = \frac{s_n}{2} \cot\left( \tfrac{\pi}{n} \right), \quad R_n = \frac{s_n}{2} \csc\left( \tfrac{\pi}{n} \right) \] 따라서 정 $n$각형의 내접원과 외접원의 반지름 길이의 비는 다음과 같이 구해진다. \[ \frac{R_n}{r_n} = \frac{\frac{s_n}{2} \csc\left( \tfrac{\pi}{n} \right)}{\frac{s_n}{2} \cot\left( \tfrac{\pi}{n} \right)} = \sec\left( \tfrac{\pi}{n} \right) \] 위 식을 살펴 보면 반지름의 비 $R_n/r_n$은 $s_n$에 의존하지 않는다는 사실을 확인할 수 있다. 또한 임의의 $n \geq 3$에 대하여, $R_n = r_{n+1}$이 성립한다. 그러므로 가장 안쪽 원의 반지름과 가장 바깥쪽원의 반지름의 비를 $K$라 하면, $K$는 다음 극한을 이용하여 구할 수 있다. \[ \begin{align*} K &= \lim_{n \to \infty} \frac{R_n}{r_3} \\[5px] &= \lim_{n \to \infty} \frac{R_3}{r_3} \frac{R_4}{r_4} \cdots \frac{R_n}{r_n} \\[5px] &= \lim_{n \to \infty} \sec\left( \tfrac{\pi}{3} \right) \sec\left( \tfrac{\pi}{4} \right) \cdots \sec\left( \tfrac{\pi}{n} \right) \\[5px] &= \prod_{n=3}^{\infty} \sec\left( \tfrac{\pi}{n} \right) \end{align*} \] 이제 위 식의 양변에 로그를 씌우면 \[ \ln(K) = \sum_{n=3}^{\infty} \ln \left( \sec\left( \tfrac{\pi}{n} \right) \right) \] 를 얻는다.

$ $

다음으로 함수 $f(x) = x^2 - \ln(\sec(x))$를 정의하자. 그러면 $f(0) = 0$이고 구간 $[0,\, \tfrac{\pi}{3}]$에서 $f'(x) > 0$이므로, 구간 $[0,\, \tfrac{\pi}{3}]$에서 $\ln(\sec(x)) \leq x^2$임을 알 수 있다. 따라서 \[ \begin{align*} \ln(K) &= \sum_{n=3}^{\infty} \ln \left( \sec\left( \tfrac{\pi}{n} \right) \right) \\[5px] &\leq \sum_{n=3}^{\infty} \left( \frac{\pi}{n} \right)^2 \\[5px] &= \pi^2 \left( \frac{\pi^2}{6} - \frac{5}{4} \right) \approx 3.8978 \end{align*} \] 즉, $\ln(K)$에 대한 무한급수는 양항급수이면서 위로 유계라는 사실로부터 수렴함을 알 수 있고, 따라서 $K$에 대한 무한곱 또한 수렴함을 알 수 있다.

$ $

$K$의 정확한 값은 알려져 있지 않지만, 컴퓨터를 이용하여 $K$ 값을 얼마든지 정확한 값에 가깝게 근사할 수 있다. 실제로 $K$의 값을 컴퓨터를 이용하여 구해보면 약 \[ K = 8.700036625\cdots \] 라는 값을 얻는다. 즉, 제일 안쪽의 원의 반지름을 $1$이라 가정하면 제일 바깥쪽에 그려지게 될 원의 반지름은 약 $8.7$이 됨을 알 수 있다. 이 $K$의 값을 외접 다각형 상수_{(polygon circumscribing constant)}라 한다.

$ $

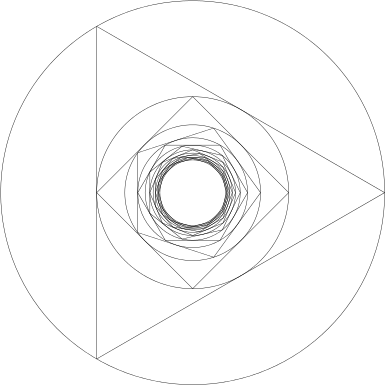
마찬가지 방법으로 두번째 문제를 해결해 보자. 아래 그림은 제일 바깥쪽의 원에서 시작해서 정 $12$각형에 내접하는 원까지를 그린 그림이다.

$ $

$ $

이제 앞서 경우와 같이 정 $n$각형의 외접원과 내접원의 반지름을 각각 $R_n$과 $r_n$으로 정의하자. 그러면 임의의 $n \geq 3$에 대하여, $r_n = R_{n+1}$이 성립한다. 따라서 가장 바깥쪽 원의 반지름과 가장 안쪽 원의 반지름의 비를 $k$라 하면, $k$는 다음 극한을 이용하여 구할 수 있다. \[ \begin{align*} k &= \lim_{n \to \infty} \frac{r_n}{R_3} \\[5px] &= \lim_{n \to \infty} \frac{r_3}{R_3} \frac{r_4}{R_4} \cdots \frac{r_n}{R_n} \\[5px] &= \lim_{n \to \infty} \cos\left( \tfrac{\pi}{3} \right) \cos\left( \tfrac{\pi}{4} \right) \cdots \cos\left( \tfrac{\pi}{n} \right) \\[5px] &= \prod_{n=3}^{\infty} \cos\left( \tfrac{\pi}{n} \right) = \frac{1}{K} \end{align*} \] 즉, $k$와 $K$는 서로 역수 관계이다. 따라서 \[ k = \frac{1}{K} \approx 0.114942045\cdots \] 를 얻는다. 즉, 제일 바깥쪽 원의 반지름을 $1$이라 가정하면 제일 안쪽에 그려지게 될 원의 반지름은 약 $0.115$가 됨을 알 수 있다. 이 $k$의 값을 내접 다각형 상수_{(polygon inscribing constant)}라 한다.