$\newcommand{\Int}{\operatorname{int}} \newcommand{\Cl}{\operatorname{cl}}$위상공간 $(X,\, \mathcal{T})$에서 정의된 집합 $A \subset X$에 대하여, $\Int(A)$와 $\Cl(A)$를 각각 $A$의 내부_(interior)와 폐포_(closure)라 하자.

$ $

$ $

일반화된 열린집합의 정의에 의해서 일반화된 연린집합들 사이에 다음과 같은 포함관계가 성립함을 간단히 확인해 볼 수 있다.

$ $

$ $

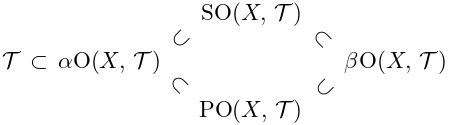
실위상공간 $(\mathbb{R},\, \mathcal{U})$에서 정의되는 일반화된 연립집합들의 예를 확인해보자.

$ $

예제. 실위상공간 $(\mathbb{R},\, \mathcal{U})$에 대하여

1. $A = (0, 1]$로 정의하면 $A$는 열린집합이 아니지만, \[ \Int(A) = (0, 1) \implies \Cl(\Int(A)) = [0, 1] \] 이므로 $A \subset \Cl(\Int(A))$가 성립하고, 따라서 $A$는 준열린집합이다.하지만 \[ \Cl(A) = [0, 1] \implies \Int(\Cl(A)) = (0, 1) \] 이므로 $A \not\subset \Int(\Cl(A))$임을 알 수 있고, 따라서 $A$는 선열린집합은 아님을 알 수 있다.
2. $A = (0, 1) \cap \mathbb{Q}$로 정의하면 $A$는 열린집합이 아니지만, \[ \Cl(A) = [0, 1] \implies \Int(\Cl(A)) = (0, 1) \] 이므로 $A \subset \Int(\Cl(A))$가 성립하고, 따라서 $A$는 선열린집합이다. 하지만 \[ \Int(A) = \emptyset \implies \Cl(\Int(A)) = \emptyset \] 이므로 $A \not\subset \Cl(\Int(A))$임을 알 수 있고, 따라서 $A$는 준열린집합은 아님을 알 수 있다.

3. $B = \{\tfrac{1}{n} : n \in \mathbb{N}\}$라 하고, $A = (-1, 1) \setminus B$로 정의하자. 그러면 $0 \in A$이지만 $0$의 어떠한 열린근방도 $A$에 포함되지 않으므로 $A$는 열린집합이 아니다. 하지만 $\Cl(B) = B \cup \{0\}$이라는 사실을 이용하면, \[ \begin{align*} \Int(A) & = \Int \big( (-1, 1) \cap B^{\,c} \big) = \Int \big( (-1, 1) \big) \cap \Int(B^{\,c}) \\[1ex] & = (-1, 1) \cap \Cl(B)^{c} = (-1, 1) \setminus \big[ B \cup \{0\} \big] \end{align*} \] 을 얻는다. 따라서 \[ \Cl(\Int(A)) = [-1, 1] \implies \Int(\Cl(\Int(A))) = (-1, 1) \] 을 각각 얻는다. 그러므로 $A \subset \Int(\Cl(\Int(A)))$가 성립하고, $A$는 $\alpha$-열린집합임을 알 수 있다.
4. $A = [0, 1] \cap \mathbb{Q}$로 정의하면 $A$는 열린집합이 아니다. 또한 \[ \begin{align*} & \Int(A) = \emptyset \implies \Cl(\Int(A)) = \emptyset \implies \Int(\Cl(\Int(A))) = \emptyset \\[1ex] & \Cl(A) = [0, 1] \implies \Int(\Cl(A)) = (0, 1) \implies \Cl(\Int(\Cl(A))) = [0, 1] \end{align*} \] 으로부터 $A \not\subset \Cl(\Int(A))$, $A \not\subset \Int(\Cl(A))$이므로 $A$는 준열린집합도 아니고 선열린집합도 아니다. 반면 $A \subset \Cl(\Int(\Cl(A)))$가 성립하므로, $A$는 $\beta$-열린집합이다.

$ $

일반화된 열린집합을 정의하는 다양한 동치명제가 존재한다. 그 중에서 몇 가지 형태적 유사성을 띄는 동치명제들을 알아보자. 증명을 위해서 먼저 다음의 보조정리가 필요하다.

$ $

$ $

증명.

1. $x \in \Cl(A) \cap U$라 가정하자. 그러면 $x \in \Cl(A)$이므로 $x_n \to x$를 만족하는 적당한 수열 $(x_n) \in A$를 택할 수 있다. 한 편, $x \in U$이고 $U$가 열린집합이라는 사실로부터 충분히 큰 자연수 $N \in \N$이 존재하여, 모든 $n \geq N$에 대하여 $x_n \in U$가 성립한다. 따라서 $n \geq N$에 대하여 $x_n \in A \cap U$이고 $x_n \to x$이므로, $x \in \Cl(A \cap U)$를 얻고, 따라서 $\Cl(A) \cap U \subset \Cl(A \cap U)$가 성립한다.
2. $K$가 닫힌집합이므로 $K^c$는 열린집합이다. 따라서 (i)에 의해 \[ \begin{align*} \big( \Int(A) \cup K \big)^c & = \Int(A)^c \cap K^c = \Cl(A^c) \cap K^c \\[1ex] & \subset \Cl(A^c \cap K^c) = \Cl \big( (A \cup K)^c \big) = \Int(A \cup K)^c. \end{align*} \] 이제 위 식의 양변에 여집합을 취하면, $\Int(A \cup K) \subset \Int(A) \cup K$가 성립함을 알 수 있다.$ $

$ $

$ $

증명.

(a) $\Leftrightarrow$ (a') 우선 $A \subset \Cl(\Int(A))$가 성립한다고 가정하자. 이제 $U = \Int(A)$를 택하면 $U$는 열린집합이고, \[ U = \Int(A) \subset A \subset \Cl(\Int(A)) = \Cl(U) \] 를 얻는다. 역으로 $U \subset A \subset \Cl(U)$를 만족하는 열린집합 $U$가 존재한다고 가정하자. 그러면 $U$는 $A$에 포함되는 열린집합이므로, $U \subset \Int(A)$가 성립한다. 따라서 $A \subset \Cl(U) \subset \Cl(\Int(A))$가 되어 $A$는 준열린집합임을 알 수 있다.

$ $

(b) $\Leftrightarrow$ (b') 우선 $A \subset \Int(\Cl(A))$가 성립한다고 가정하자. 이제 $U = \Int(\Cl(A))$를 택하면 $U$는 열린집합이고 $U \subset \Cl(A)$가 성립한다. 따라서 \[ A \subset \Int(\Cl(A)) = U \subset \Cl(A) \] 를 얻는다. 역으로 $A \subset U \subset \Cl(A)$를 만족하는 열린집합 $U$가 존재한다고 가정하자. 그러면 $U$는 $\Cl(A)$에 포함되는 열린집합이므로, $U \subset \Int(\Cl(A))$가 성립한다. 따라서 $A \subset U \subset \Int(\Cl(A))$가 되어 $A$는 선열린집합임을 알 수 있다.

$ $

(c) $\Leftrightarrow$ (c') 우선 $A \subset \Int(\Cl(\Int(A)))$가 성립한다고 가정하자. $U = \Int(A)$로 정의하면 $U$는 열린집합이고 \[ U \subset A \subset \Int(\Cl(\Int(A))) = \Int(\Cl(U)) \] 가 성립한다. 역으로 $U \subset A \subset \Int(\Cl(U))$를 만족하는 열린집합 $U$가 존재한다고 가정하자. 그러면 $U$는 $A$에 포함되는 열린집합이므로, $U \subset \Int(A)$가 성립한다. 따라서 \[ A \subset \Int(\Cl(U)) \subset \Int(\Cl(\Int(A))) \] 가 되어 $A$는 $\alpha$-열린집합임을 알 수 있다.

$ $

(c) $\Leftrightarrow$ (c'') 우선 $A \subset \Int(\Cl(\Int(A)))$가 성립한다고 가정하자. $U = \Int(\Cl(\Int(A)))$로 정의하면 $U$는 열린집합이고 \[ A \subset U \subset \Cl(\Int(A)) \] 가 성립한다. 역으로 $A \subset U \subset \Cl(\Int(A))$를 만족하는 열린집합 $U$가 존재한다고 가정하자. 그러면 $U \subset \Int(\Cl(\Int(A)))$가 성립하므로, $A \subset \Int(\Cl(\Int(A)))$가 되어 $A$는 $\alpha$-열린집합임을 알 수 있다.

$ $

(d) $\Leftrightarrow$ (d') 우선 $A \subset \Cl(\Int(\Cl(A)))$가 성립한다고 가정하자. 이제 $G = A \cup \Int(\Cl(A))$를 택하자. 먼저 $G$는 준열린집합임을 보일 것이다. 임의의 집합 $C,\, D$에 대하여 $\Int(C \cup D) \supset \Int(C) \cup \Int(D)$가 성립하므로, \[ \Int(G) = \Int \big( A \cup \Int(\Cl(A)) \big) \supset \Int(A) \cup \Int(\Cl(A)) = \Int(\Cl(A)) \] 를 얻는다. 따라서 $\Int(\Cl(A)) \subset \Int(G) \subset \Cl(\Int(G))$임을 알 수 있다. 한 편, 주어진 가정으로부터 $A \subset \Cl(\Int(\Cl(A))) \subset \Cl(\Int(G))$라는 사실 또한 얻을 수 있다. 이제 이 두 식을 종합하면, \[ G = A \cup \Int(\Cl(A)) \subset \Cl(\Int(G)) \] 가 되어 $G$는 준열린집합이다. 이제 $A \subset \Cl(A)$, $\Int(\Cl(A)) \subset \Cl(A)$라는 사실로부터, \[ A \subset G = A \cup \Int(\Cl(A)) \subset \Cl(A) \] 가 되어 원하는 결론을 얻는다. 이제 역으로 $A \subset G \subset \Cl(A)$를 만족하는 준열린집합 $G$가 존재한다고 가정하자. 그러면 $G \subset \Cl(\Int(G))$가 성립하므로, \[ A \subset G \subset \Cl(\Int(G)) \subset \Cl(\Int(\Cl(A))) \] 가 되어 $A$는 $\beta$-열린집합임을 알 수 있다.

$ $

(d) $\Leftrightarrow$ (d'') 우선 $A \subset \Cl(\Int(\Cl(A)))$가 성립한다고 가정하자. 이제 $H = A \cap \Int(\Cl(A))$를 택하자. 먼저 $H$가 선열린집합임을 보일 것이다. $\Int(\Cl(A))$은 자명하게 열린집합이므로 보조정리.(i)에 의해 \[ \Cl(H) = \Cl \big( A \cap \Int(\Cl(A)) \big) \supset \Cl(A) \cap \Int(\Cl(A)) = \Int(\Cl(A)) \] 를 얻는다. 따라서 $\Int(\Cl(A)) \subset \Int(\Cl(H))$임을 알 수 있다. 그러므로 \[ H = A \cap \Int(\Cl(A)) \subset \Int(\Cl(A)) \subset \Int(\Cl(H)) \] 가 성립하고 $H$는 선열린집합이다. 이제 주어진 가정으로부터 \[ H = A \cap \Int(\Cl(A)) \subset A \subset \Cl(\Int(\Cl(A))) \subset \Cl(\Int(\Cl(H))) \subset \Cl(H) \] 가 되어 원하는 결론을 얻는다. 이제 역으로 $H \subset A \subset \Cl(H)$를 만족하는 선열린집합 $H$가 존재한다고 가정하자. 그러면 $H \subset \Int(\Cl(H))$가 성립하므로, \[ A \subset \Cl(H) \subset \Cl(\Int(\Cl(H))) \subset \Cl(\Int(\Cl(A))) \] 가 되어 $A$는 $\beta$-열린집합임을 알 수 있다.$ $