유리수의 집합 $\Q$가 셀수 있는 집합임을 잘 알려져 있다. 이를 다시 표현하면 "모든 유리수를 단 한번씩 포함하는 수열"을 구성하는 것이 가능하다는 말이 된다. 이러한 수열을 구성하는 가장 간단한 방법은 아래와 같다.

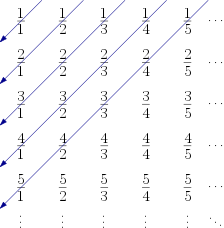
즉, 모든 양의 정수 $i,\, j$에 대하여 $(i,\,j)$-원소가 $\frac{i}{j}$인 무한행렬을 만들고 이 행렬의 원소를 왼쪽 위에서부터 화살표가 나타내는 대각선 방향으로 읽어 내려가는 것이다. 그렇게 하면 \[ \frac{1}{1},\, \frac{1}{2},\, \frac{2}{1},\, \frac{1}{3},\, \textcolor{red}{\frac{2}{2}},\, \frac{3}{1},\, \frac{1}{4},\, \frac{2}{3},\, \frac{3}{2},\, \frac{4}{1},\, \frac{1}{5},\, \textcolor{red}{\frac{2}{4}},\, \textcolor{red}{\frac{3}{3}},\, \textcolor{red}{\frac{4}{2}},\, \frac{5}{1},\, \ldots \] 를 얻는다. 하지만 위에서 붉은색으로 표현된 항들은 모두 앞선 항과 중복이므로 이를 모두 제외한 \[ \frac{1}{1},\, \frac{1}{2},\, \frac{2}{1},\, \frac{1}{3},\, \frac{3}{1},\, \frac{1}{4},\, \frac{2}{3},\, \frac{3}{2},\, \frac{4}{1},\, \frac{1}{5},\, \frac{5}{1},\, \ldots \] 가 우리가 원하는 모든 유리수를 단 한번씩 포함하는 수열이 된다.

$ $

위 수열의 구성 방법의 가장 큰 단점은 어떤 항이 이미 앞선 항에 표현되어 있는지의 여부를 간단히 알 수 없다는 데 있다. 간단히 표현하자면, 어떤 항에 있는 분수 표현에서 분자와 분모에 공약수가 존재한다면, 이 항은 이미 앞선 항에 등장했다는 사실을 알 수 있다. 하지만 예를 들어 \[ \frac{3,915,059}{39,177,995,413} \] 와 같은 큰 분수의 경우, 분자와 분모에 공약수가 존재하는지를 확인하는 것은 간단한 일은 아닐 것이다.¹ 이와 같은 단점을 해결하면서 "모든 유리수를 단 한번씩 포함하는 수열"을 구성하는 것이 가능할까?

$ $

다음과 같이 Calkin-Wilf 나무 그래프_{(tree graph)}를 정의하자.

1. 그래프 제일 위쪽의 점에 $\frac{1}{1}$의 값을 할당한다.
2. 그래프에서 어떤 점에 $\frac{i}{j}$의 값이 주어졌다고 하자. 그러면 이 점은 두 개의 자식 점을 갖는데, 이 중 왼쪽 자식 점은 $\frac{i}{i+j}$의 값을, 오른쪽 자식 점은 $\frac{i+j}{j}$의 값을 각각 할당한다.

$ $

위 두가지 조건을 만족하는 그래프를 그러보면 다음과 같다.

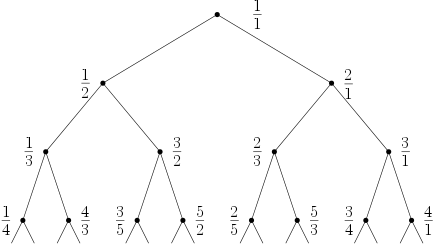
이제 위 그래프의 각 점에 주어진 모든 유리수들을 위에서 아래로, 왼쪽에서 오른쪽으로 차례로 읽어나갈 때 얻는 수열 \[ \frac{1}{1},\, \frac{1}{2},\, \frac{2}{1},\, \frac{1}{3},\, \frac{3}{2},\, \frac{2}{3},\, \frac{3}{1},\, \frac{1}{4},\, \frac{4}{3},\, \frac{3}{5},\, \frac{5}{2},\, \frac{2}{5},\, \frac{5}{3},\, \frac{3}{4},\, \frac{4}{1},\, \ldots \tag*{$\myblue{(\ast)}$} \] 은 놀랍게도 "모든 유리수를 단 한번씩 포함하는 수열"이 된다. 이 사실을 직접 증명해 보자.

$ $

$ $

증명. 결론에 반하여 어떤 점 $p$에 할당 된 $\frac{i}{j}$가 약분이 된다고 가정해 보자. 여기서 $p$에 할당된 분수가 $\frac{1}{1}$일 수는 없으므로, 어떤 점 $q$의 자식 점이 되어야만 한다. 따라서 $q$에 할당된 분수는 $\frac{i}{j-i}$이거나 $\frac{i-j}{j}$임을 알 수 있다. 하지만 $i$와 $j$에 공약수가 존재하므로 두 경우 모두 기약분수가 아님을 알 수 있다. 즉, 어떤 점에 약분이 가능한 분수가 할당 되었다면 그 점의 부모 점에 할당된 분수 또한 약분이 가능하다. 따라서 수학적 귀납법에 의해 제일 윗 점에 할당된 $\frac{1}{1}$이 약분 가능해야 하는데 이는 모순이다. 따라서 모든 점에 해당된 분수는 모두 기약분수이다..

$ $

$ $

증명. 결론에 반하여 그래프에 등장하지 않는 기약분수가 존재한다고 가정하자. 그러한 기약분수들 중 분모가 가장 작고, 그 중에서 분자 또한 가장 작은 분수를 $\frac{i}{j}$라 하자. 만약 $i > j$인 경우, $\frac{i-j}{j}$ 또한 그래프에 등장하지 않아야만 한다. 만약 $\frac{i-j}{j}$가 할당된 점이 존재한다면, 이 점의 오른쪽 자식 점에 $\frac{i}{j}$가 할당되기 때문이다. 하지만 자명하게 $i-j < i$가 성립하므로 $\frac{i}{j}$가 분자가 가장 작다는데 모순이 발생한다. 역으로 $i < j$인 경우, 비슷한 $\frac{i}{j-i}$ 또한 그래프에 등장하지 않아야만 함을 알 수 있다. 하지만 이 경우 역시 $\frac{i}{j}$가 분모가 가장 작다는데 모순이 발생한다. 어떤 경우에도 모순이 발생하므로, 모든 기약분수는 그래프에 적어도 한 번은 등장해야 한다..

$ $

$ $

증명. 만약에 동일한 기약분수가 할당된 두 개 이상의 점이 존재한다면, 그 점들의 부모 점들에 할당된 기약분수 또한 동일하므로, 수학적 귀납법에 의해 결국 제일 윗 점에 할당 된 $\frac{1}{1}$이 단 한 번만 등장함을 증명하면 충분함을 알 수 있다. 이제 $\frac{1}{1}$이 제일 윗 점이 아닌 다른 점 $p$에도 할당 된다고 가정해 보자. 그러면 $p$의 부모 점 $q$에 할당 된 $\frac{i}{j}$에 대하여 $\frac{1}{1} = \frac{i}{i+j}$이거나 $\frac{1}{1} = \frac{i+j}{j}$여야 한다. 하지만 위 조건을 만족하는 $i,\,j$는 존재하지 않으므로 모순임을 알 수 있다. 따라서 모든 기약분수는 그래프에 많아야 한 번 등장한다..

$ $

따라서 위 세 명제를 종합하면, Calkin-Wilf 나무 그래프에는 모든 기약분수가 정확히 한 번 씩 등장함을 알 수 있다. 한 편, 수열 $\myblue{(\ast)}$의 인접한 두 항 사이에는 재미있는 관계가 존재하는데, 바로 어떤 항의 분모는 바로 그 다음 항의 분자가 된다는 사실이다.

$ $

따라서 다음과 같이 수열 $\myblue{(\ast)}$의 각 항의 분자 \[ 1,\, 1,\, 2,\, 1,\, 3,\, 2,\, 3,\, 1,\, 4,\, 3,\, 5,\, 2,\, 5,\, 3,\, 4,\, \ldots \] 만으로도 수열 $\myblue{(\ast)}$ 전체를 얻을 수 있다. (OEIS-A002487) 이 수열을 $(a_n)_{n \geq 1}$으로 나타내기로 하자. 그러면 우리가 원하는 유리수 수열은 $(\tfrac{a_n}{a_{n+1}})_{n \geq 1}$으로 나타낼 수 있다. 한 편, 다시 한 번 나무 그래프를 구성했던 방법을 떠올려 보면 어떤 점 $\tfrac{a_n}{a_{n+1}}$의 두 자식 점은 각각 $\tfrac{a_{2n}}{a_{2n+1}}$과 $\tfrac{a_{2n+1}}{a_{2n+2}}$이 되어야 한다. 따라서 부모 점과 자식 점 사이의 관계에 의해서 다음의 점화식_{(recursive relation)} \[ a_{2n} = a_n, \quad a_{2n+1} = a_{n} + a_{n+1}, \quad a_1 = a_2 = 1 \] 을 얻는다.