좌표평면에서 격자점(lattice point)이란 좌표 $(x,\, y)$가 모두 정수인 점을 뜻한다. 이제 양의 정수 $n$에 대하여 정확하게 $n$개의 격자점을 지나는 원을 생각해 보자. 우선 $n=1$인 경우 간단히 $(3x-1)^2 + 9y^2 = 1$을 생각해 보면 $(\frac{1}{3},\, 1)$이고 반지름이 $\frac{1}{3}$인 원이므로 정확히 $1$개의 격자점 $(0,\,0)$을 지나는 것을 알 수 있다. 또한 $n=2$인 경우에는 원 $(2x-1)^2 + 4y^2 = 1$를 생각해 보면 중심이 $(\frac{1}{2},\, 1)$이고 반지름이 $\frac{1}{2}$인 원이므로 정확히 $2$개의 격자점 $(0,\, 0)$과 $(1, 0)$을 지남을 알 수 있다. 이와 같은 방법으로 $n=3,\, 4,\, 5,\, \ldots$인 경우에도 정확히 $n$개의 격자점을 지나는 원이 언제나 존재할까?
이 문제는 Schinzel에 의해 해결되었는데 이번 글에서는 Schinzel의 정리에 대해서 살펴 보고자 한다.
증명. 가우스 정수환 $\Z[i]$ 위에서 $5$를 인수분해 하면, $5 = (1 + 2i)(1-2i)$를 얻고
를 얻는다. 따라서 임의의 $0 \leq j \leq k$에 대하여,
여기서 $a_{j},\, b_{j} > 0$이다. 이제 $j$를 선택하는 경우의 수는 $k+1$이고, 각각의 선택된 $j$에 대하여
의 네가지 서로 다른 해를 얻을 수 있으므로, $x^2 + y^2 = 5^k$를 만족하는 정수해의 개수는 $4(k+1)$개임을 알 수 있다..
이제 위 보조정리를 이용하여 Schinzel의 정리를 증명해 보자.
증명. 먼저 $n=2k$를 가정하자. 그러면 보조정리에 의해 방정식 $x^2 + y^2 = 5^{k-1}$은 정확히 $4k$개의 정수해를 갖는다. 이제 $5^{k-1}$은 홀수이기 때문에, 위 방정식의 정수해 $(x,\, y)$에서 $x$와 $y$ 중 오직 하나만이 홀수여야 함을 알 수 있다. 따라서 $x$는 홀수이고 $y$는 짝수여야 한다는 조건을 추가하면, 총 $4k$개의 해 중의 절반인 $2k$개의 해를 얻을 수 있다. 따라서 방정식
는 정확히 $2k = n$개의 정수해를 갖는다.
이제 $n = 2k-1$이라 가정하자. 그러면 보조정리에 의해 방정식 $x^2 + y^2 = 5^{2(k-1)}$는 정확히 $4(2k-1)$개의 해를 갖는다. 이제 임의의 양의 정수 $m$에 대하여 $m^2 \equiv 0,\,1 \pmod{3}$이고 $5^{2k} \equiv 1 \pmod{3}$이 성립하기 때문에, 위 방정식의 정수해 $(x,\, y)$에서 $x$와 $y$ 중 오직 하나만이 $3$의 배수임을 알 수 있다. 따라서 $y$가 $3$의 배수여야 한다는 조건을 추가하면, 총 $4(2k-1)$개의 해 중의 절반인 $2(2k-1)$개의 해를 얻을 수 있다. 이제 정수해 $(x,\,y)$는
의 형태를 갖는다. 하지만 $(3u-1,\, 3v)$ 형태의 정수해 집합과 $(3u'+1,\, 3v)$ 형태의 정수해 집합 사이에는 $u = -u'$의 일대일 대응이 존재한다. 따라서 $x = 3u - 1$ 꼴이라는 조건을 추가하면, $2(2k-1)$개의 해 중 절반인 $2k-1 = n$개의 해를 얻을 수 있다. 따라서 방정식
은 정확히 $2k-1 = n$개의 정수해를 갖는다..
위 공식을 적용하면, $n = 1,\, 2,\, \ldots,\, 6$개의 격자점을 지나는 원의 방정식은 각각
로 주어지고 이를 좌표평면 위에 나타내면
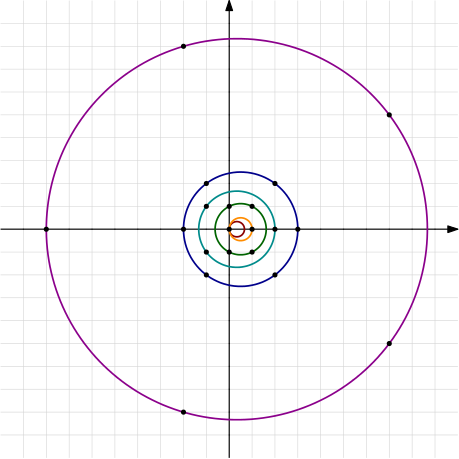
를 얻는다.
참고. Schinzel의 구성한 원들은 정확하게 $n$개의 격자점을 지나기는 하지만, 이를 만족하는 원들 중에 반지름이 최소는 아니다. 예를 들어 $n=4$인 경우, Schinzel의 원은 반지름이 $\frac{\sqrt{5}}{2}$이다. 하지만 $x^2 + y^2 = 1$ 또한 정확히 $4$개의 격자점을 지나고 반지름이 $1$임을 알 수 있다. 또한 $(x - \frac{1}{2})^2 + (y - \frac{1}{2})^2 = \frac{1}{2}$ 또한 정확히 $4$개의 격자점을 지나는데, 이 때의 반지름은 $\frac{\sqrt{2}}{2}$ 밖에는 되지 않는다. (사실, 이 원이 정확히 $4$개의 격자점을 지나는 최소의 반지름을 갖는 원이다.)
Schinzel의 정리를 3차원으로 확장한 Kulikowski의 정리가 있는데, 이는 다음과 같다.