$\DeclareMathOperator{\lcm}{lcm}$이번 포스트에서는 자연수 집합 위에 자연수의 소인수분해와 밀접한 관련이 있는 거리_(distance)을 정의해 볼 것이다. 우선 실수 집합 위에서 정의된 유클리드 거리_{(Euclidean distance)}를 이용하여 두 자연수 $12$과 $13$ 사이의 거리를 구해보면, $\abs{12 - 13} = 1$임을 쉽게 알 수 있다. 이번에는 두 자연수 $12$와 $18$을 생각해 보자. 이 두 자연수의 유클리드 거리는 $\abs{12 - 18} = 6$이지만, 자연수의 관점에서 본다면 두 자연수 $12$와 $13$ 사이의 거리 보다는 $12$와 $18$ 사이의 거리가 더 가깝다고 주장할 수 있다. $12$와 $18$이 더 많은 소인수를 공유하고 있기 때문이다. 이와 같은 관점을 반영하여 다음과 같이 자연수 집합 위에 산술거리_{(arithmetic distance)}을 정의하고 그 성질을 알아볼 것이다.

$ $

자연수의 집합을 $\mathbb{N}$으로, 소수의 집합을 $\mathbb{P}$로 각각 나타내기로 하자. 그러면 자연수 $n \in \mathbb{N}$과 소수 $p \in \mathbb{P}$에 대하여 $n$의 $p$진 값매김_{($p$-adic valuation)}을 다음과 같이 정의한다. \[ \nu_{p}(n) = \max \set{k \geq 0}{p^k \,|\, n}. \] 즉, $\nu_{p}(n)$이란 주어진 $n$을 소수 $p$로 최대 몇 번까지 나눌 수 있는지를 알려주는 함수이다. 또한 산술의 기본정리_{(fundamental theorem of arithmetic)}에 의하면 임의의 자연수 $n$은 유일한 소인수분해를 가지는데, 이때의 소인수분해를 $p$진 값매김을 이용하여 \[ n = \prod_{p \in \mathbb{P}} p^{\nu_{p}(n)} \] 와 같이 나타낼 수 있다. 이를 이용하여 두 자연수 $m,\, n \in \N$ 사이의 산술거리_{(arithmetic distance)}를 다음과 같이 정의하자.

$ $

$ $

예를 들어 두 자연수 $12 = 2^2 \cdot 3^1$와 $18 = 2^1 \cdot 3^2$의 산술거리는 다음과 같이 \[ d(12,\, 18) = \abs{\nu_{2}(12) - \nu_{2}(18)} + \abs{\nu_{3}(12) - \nu_{3}(18)} = \abs{2 - 1} + \abs{1 - 2} = 2 \] 와 같이 계산된다. 반면 $d(12,\, 13) = 4$이므로, 자연수의 소인수분해의 관점에서 $12$와 $13$ 사이의 거리 보다는 $12$와 $18$ 사이의 거리가 더 가까워야 할 것이라는 우리의 직관과 잘 맞아떨어진다.

$ $

위에서 정의한 산술거리함수가 실제로 거리함수_(metric)가 된다는 사실은 정의로부터 자명함을 알 수 있다. 이제 산술거리함수의 여러가지 성질을 증명하는데 중요한 도구가 될 정리를 하나 살펴보자. 우선 주어진 $n \in \mathbb{N}$의 소인수분해에서 나타나는 (중복을 포함한) 모든 소인수의 개수를 나타내는 함수를 생각해 보자. 이 함수는 다음과 같이 \[ \Omega(n) = \sum_{p \in \mathbb{P}} \nu_{p}(n) \] 로 나타낼 수 있다. 이 함수를 정수론에서는 소인수계량함수_{(prime omega function)}이라 한다. 이 함수는 완전가법적_{(completely additive)}임이 잘 알려져 있다. 즉, 임의의 자연수 $m,\, n \in \mathbb{N}$에 대하여, \[ \Omega(mn) = \Omega(m) + \Omega(n) \] 이 성립한다. (이는 산술의 기본정리를 생각해보면 간단히 성립함을 확인해 볼 수 있다.)다음 정리는 산술거리함수를 소인수계량함수를 이용하여 표현할 수 있음을 보여준다. 이제 두 자연수 $m,\, n \in \N$의 최소공배수와 최대공약수를 각각 $\lcm(m,\, n)$과 $\gcd(m,\, n)$으로 나타내면 $m$과 $n$의 산술거리를 소인수계량함수를 이용하여 다음과 같이 나타낼 수 있다.

$ $

$ $

증명. 먼저 최소공배수와 최대공약수를 $p$진 값매김을 이용하여 다음과 같이 표현 가능함을 확인해 보자. \[ \begin{align*} \lcm(m,\, n) & = \prod_{p \in \mathbb{P}} \max \{\nu_{p}(m),\, \nu_{p}(n)\} \\[5pt] \gcd(m,\, n) & = \prod_{p \in \mathbb{P}} \min \{\nu_{p}(m),\, \nu_{p}(n)\} \end{align*} \] 이 사실을 이용하면, \[ \begin{align*} \Omega(\lcm(m,\, n)) & - \Omega(\gcd(m,\, n)) \\[5pt] & = \prod_{p \in \mathbb{P}} \max \{\nu_{p}(m),\, \nu_{p}(n)\} - \min \{\nu_{p}(m),\, \nu_{p}(n)\} \\[5pt] & = \sum_{p \in \mathbb{P}} \abs{\nu_{p}(m) - \nu_{p}(n)} \\[5pt] & = d(m,\, n). \tag*{$\myblue{\blacksquare}$} \end{align*} \]

$ $

따라서 $\lcm(12,\, 18) = 36$, $\gcd(12,\, 18) = 6$이라는 사실로부터, \[ d(12,\, 18) = \Omega(36) - \Omega(6) = 4 - 2 = 2 \] 와 같이 계산할 수 있다.

$ $

$ $

증명. $m$과 $n$이 서로소이므로, $\lcm(m,\, n) = mn$, $\gcd(m,\, n) = 1$이 성립한다. 따라서 정리 1과 $\Omega$의 완전가법성에 의해, \[ \begin{align*} d(m,\, n) & = \Omega(\lcm(m,\, n)) - \Omega(\gcd(m,\, n)) \\[5pt] & = \Omega(mn) - \Omega(1) \\[5pt] & = \Omega(m) + \Omega(n) - \Omega(1) \\[5pt] & = \Omega(m) + \Omega(n) \end{align*} \] 을 얻는다. 특히 임의의 자연수 $n \in \N$에 대하여 $n$과 $1$은 서로소이므로, \[ d(n,\, 1) = \Omega(n) + \Omega(1) = \Omega(1) \] 이 성립한다.$ $

$ $

두 자연수 $m,\, n \in \mathbb{N}$가 서로소가 아닌 경우, 즉, 공통인수 $k \in \N$가 존재하는 경우에는, 다음 정리를 이용하여 $d(m,\, n)$의 계산을 좀 더 간단히 할 수 있다.

$ $

$ $

증명. 정리 1과 $\Omega$의 완전가법성에 의해 다음을 얻는다. \[ \begin{align*} d(km, kn) & = \Omega(\lcm(km,\, kn)) - \Omega(\gcd(km,\, kn)) \\[5pt] & = \Omega(k\lcm(m,\, n)) - \Omega(k\gcd(m,\, n)) \\[5pt] & = \big[ \Omega(k) + \Omega(\lcm(m,\, n)) \big] - \big[ \Omega(k) + \Omega(\gcd(m,\, n)) \big] \\[5pt] & = \Omega(\lcm(m,\, n)) - \Omega(\gcd(m,\, n)) \\[5pt] & = d(m,\, n) \tag*{$\myblue{\blacksquare}$} \end{align*} \]

$ $

따라서 $d(12,\, 18)$의 경우, 다음과 같이 정리 2와 정리 3을 적용하여 \[ d(12,\, 18) = d(2,\, 3) = \Omega(2) + \Omega(3) = 1 + 1 = 2 \] 로 계산이 가능하다.

$ $

$ $

증명. $m = gm_{0}$, $n = gn_{0}$, $l = gm_{0}n_{0}$를 만족하는 서로소인 두 자연수 $m_{0},\, n_{0} \in \N$을 택하자. 그러면 $m^k = g^km_0^k$, $n^k = g^kn_0^k$로 나타낼 수 있다. 이제 $m_0$와 $n_0$가 서로소이므로 $m_0^k$와 $n_0^k$ 또한 서로소이다. 따라서 정리 2, 정리 3과 $\Omega$의 완전가법성에 의해 \[ \begin{align*} d(m^k,\, n^k) & = d(m_0^k,\, d_0^k) \\[5pt] & = \Omega(m_0^k) + \Omega(n_0^k) \\[5pt] & = k \big[ \Omega(m_0) + \Omega(n_0) \big] \\[5pt] & = k d(m_0,\, n_0) \\[5pt] & = k d(m,\, n). \tag*{$\myblue{\blacksquare}$} \end{align*} \]

$ $

$ $

증명. 우선 적당한 소수 $\bar{p} \in \mathbb{P}$에 대하여 $m = \bar{p}n$이 성립한다고 가정하자. 그러면 정리 1과 $\Omega$의 완전가법성에 의해 \[ \begin{align*} d(m,\, n) & = \Omega(\lcm(m,\, n)) - \Omega(\gcd(m,\, n)) \\[5pt] & = \Omega(\lcm(\bar{p}n,\, n)) - \Omega(\gcd(\bar{p}n,\, n)) \\[5pt] & = \Omega(\bar{p}n) - \Omega(n) \\[5pt] & = \Omega(\bar{p}) + \Omega(n) - \Omega(n) \\[5pt] & = \Omega(\bar{p}) \\[5pt] & = 1 \end{align*} \] 임을 알 수 있다.

이번에는 반대로 $d(m,\, n) = 1$을 가정하자. 이는 정의에 의해 \[ \sum_{p \in \mathbb{P}} \abs{\nu_{p}(m) - \nu_{p}(n)} = 1 \] 임을 뜻한다. 여기서 위 식 우변의 $\abs{\nu_{p}(m) - \nu_{p}(n)}$의 값은 모든 $p \in \mathbb{P}$에 대하여 음이 아닌 정수이므로, 적당한 $\bar{p} \in \mathbb{P}$가 존재하여, $\abs{\nu_{\bar{p}}(m) - \nu_{\bar{p}}(n)} = 1$이고 $\bar{p}$가 아닌 모든 소수 $p$에 대하여 $\abs{\nu_{p}(m) - \nu_{p}(n)} = 0$이어야만 함을 알 수 있다. 이는 $m$과 $n$의 소인수분해를 비교해 보았을 때, 소수 $\bar{p}$를 제외한 모든 소인수의 개수가 동일함을 의미한다. 이제 $m \geq n$을 가정했으므로, $m = \bar{p}n$이어야만 하고, 따라서 증명이 완료된다.$ $

$ $

$ $

증명. 주어진 가정으로부터 $m = gm_{0}$, $n = gn_{0}$, $l = gm_{0}n_{0}$를 만족하는 서로소인 두 자연수 $m_{0},\, n_{0} \in \N$을 택할 수 있다. 따라서 정리 2와 정리 3에 의해 \[ \begin{align*} d(l,\, m) & = d(gm_{0}n_{0},\, gm_{0}) = d(n_{0},\, 1) = \Omega(n_{0}) \\[5px] d(g,\, m) & = d(g,\, gm_{0}) = d(1,\, m_{0}) = \Omega(m_{0}). \\[5px] \end{align*} \] 같은 방법으로 $d(l,\, n) = \Omega(m_{0})$, $d(g,\, n) = \Omega(n_{0})$을 얻는다. 한 편, $m_{0}$와 $n_{0}$는 서로소이므로 다시 한 번 정리 2와 정리 3에 의해 \[ d(m,\, n) = d(gm_{0},\, gn_{0}) = d(m_{0},\, m_{0}) = \Omega(m_{0}) + \Omega(n_{0}). \] 그러므로 위 정리에 주어진 세 변 모두 $\Omega(m_{0}) + \Omega(n_{0})$ 값을 가짐을 알 수 있다.$ $

$ $

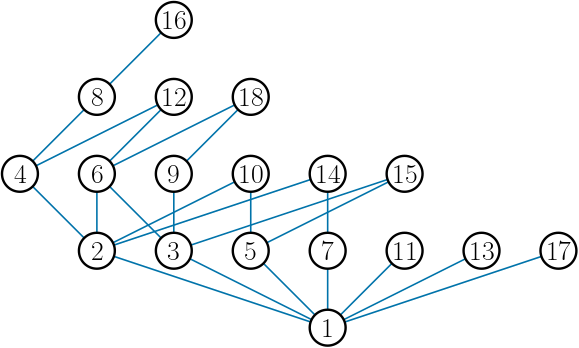
아래 그림과 같이 집합 $\{1,\, 2,\, \ldots,\, 18\}$ 위에서의 약수관계를 부분순서_{(partial order)}로 정의하고, 이에 대한 하세 도형_{(Hasse diagram)}을 생각해 보자.

$ $

$ $

이제 정리 6에 의하면, 두 자연수 $12$와 $18$ 사이의 산술거리는 위 하세 도형에서 $12$에서 $18$로 가는 최단 경로의 길이와 같음을 알 수 있다.

$ $

참고. 주어진 자연수 $n \in \N$의 소인수분해를 p진 값매김 함수를 이용하여 다음과 같이 나타내자. \[ n = \prod_{p \in \mathbb{P}} p^{\nu_{p}(n)} = 2^{\nu_2(n)} 3^{\nu_3(n)} 5^{\nu_5(n)} 7^{\nu_7(n)} \cdots. \] 그러면 소인수분해의 유일성에 의해 "자연수 집합"과 "유한개의 항을 제외한 모든 항이 $0$인 음이 아닌 정수로만 이루어진 수열들의 집합"간의 일대일대응관계를 줄 수 있다. \[ n = 2^{\nu_2(n)} 3^{\nu_3(n)} 5^{\nu_5(n)} 7^{\nu_7(n)} \cdots \; \longleftrightarrow \; \big( \nu_2(n),\, \nu_3(n),\, \nu_5(n),\, \nu_7(n),\, \ldots \big). \] 예를 들면, \[ \begin{align*} 5 \; \longleftrightarrow \; (0,\, 0,\, 1,\, 0,\, \ldots) \\[5pt] 12 \; \longleftrightarrow \; (2,\, 1,\, 0,\, 0,\, \ldots) \\[5pt] 18 \; \longleftrightarrow \; (1,\, 2,\, 0,\, 0,\, \ldots) \\[5pt] \end{align*} \] 과 같은 식이다. 이 때, 두 자연수의 산술거리는 그 자연수들과 대응관계에 있는 두 수열 사이의 유클리드 거리_{(Euclidean distance)}와 같음을 알 수 있다. \[ \begin{align*} d(m, n) & = \sum_{p \in \mathbb{P}} \abs{\nu_{p}(m) - \nu_{p}(n)} \\[5pt] & = \Big| \big( \nu_2(m),\, \nu_3(m),\, \nu_5(m),\, \nu_7(m),\, \ldots \big) - \big( \nu_2(n),\, \nu_3(n),\, \nu_5(n),\, \nu_7(n),\, \ldots \big) \Big|. \end{align*} \] 예를 들어 $12$와 $18$의 산술거리는 이 두 자연수의 대응관계에 있는 두 수열 $(2,\, 1,\, 0,\, 0,\, \ldots)$과 $(1,\, 2,\, 0,\, 0,\, \ldots)$의 유클리드 거리를 이용하여 \[ d(12,\, 18) = \big| (2,\, 1,\, 0,\, 0,\, \ldots) - (1,\, 2,\, 0,\, 0,\, \ldots) \big| = 2 \] 로 계산할 수 있다.$ $

$ $

위에서 살펴본 일대일대응 관계를 이용하여 산술거리를 유리수 집합까지 확장할 수 있는데, 이에 대한 내용은 다음 포스트에서 좀 더 자세히 알아보기로 하자.

$ $