이전 포스트에서 여러가지 공간_(space)에 대한 정의에 대해 살펴보았다. 이번 포스트에서는 각 공간들 사이에 포함관계에 대해서 알아보도록 한다.

실제로 수학에서 쓰이는 수학적 공간은 아래에 열거된 것 보다 훨씬 범위가 넓다. 예를 들어, 미분기하학에서 쓰이는 다양체_(manifold)가 있고, 미분방적식을 다룰 때에 공간은 보통 소볼레프 공간_{(Sobolev space)}을 의미한다. 측도론_{(measure theory)}에서의 측도공간_{(measure space)}도 수학적 공간의 한 예이며, 이의 특수한 경우인 확률공간_{(probability space)}는 보통 통계학에서 다루어진다. 이 외에도 위상수학_{(general topology)} 에서의 하우스도르프 공간_{(Hausdorff space)}, 정칙공간_{(regular space)}, 정규공간_{(normal space)} 등을 생각해 볼 수 있다. 이 포스트에서는 해석학, 특히 실해석학에서 주로 다루는 공간만을 다루도록 한다.

$ $

1. 거리공간(metric space) \( \subset \) 위상공간(topological space)

거리공간_{(metric space)} \( \left( M,d \right) \)에서, 점 \(x_{0} \in M \)을 중심으로 하고, 반지름 \(r \in \mathbb{R} \)을 갖는 열린 공_{(open ball)}을 다음과 같이 정의한다.

이제 열린 공들을 기저_(basis)로 갖는 위상_(topology) \( \mathcal{T} \)를 만들면, 이는 거리위상_{(distance topology)}이 되고 위상공간_{(topological space)}의 성질을 만족한다.

$ $

2. 노름공간(normed vector space) \( \subset \) 거리공간(metric space)

노름공간_{(normed vector space)} \( \left( V, || \cdot || \right) \)에서, 두 원소 \( x,y \in V \) 사이의 거리를 다음과 같이 정의한다.

그러면 \( \left( V, d \right) \)는 거리공간_{(metric space)}의 성질을 만족한다.

$ $

3. 내적공간(inner product space) \( \subset \) 노름공간(normed vector space)

내적공간_{(inner product space)} \( \left( V, \left< \cdot, \cdot \right> \right) \)에서, \(V\)의 원소 \(x\)의 노름_(norm)을 다음과 같이 정의한다.

그러면 \( \left( V, || \cdot || \right) \)는 노름공간_{(normed vector space)}의 성질을 만족한다.

$ $

4. 힐베르트 공간(Hilbert space) \( \subset \) 바나흐 공간(Banach space)

힐베르트 공간_{(Hilbert space)}은 완비내적공간_{(complete inner product space)}이고, 바나흐 공간_{(Banach space)}은 완비노름공간_{(complete normed vector space)}이므로, 3에 의해 자명하게 성립한다.

$ $

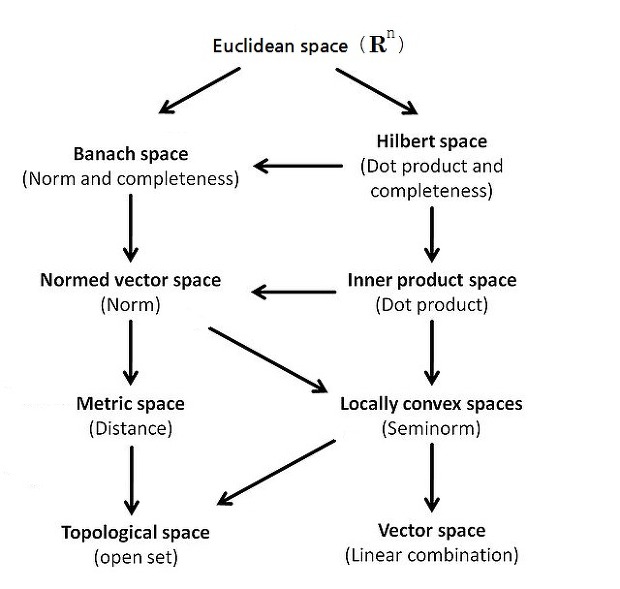
이상의 성질들을 도표로 만들면 다음과 같다.