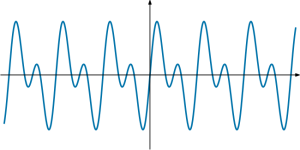
두 함수 $\sin(x)$와 $\sin(2x)$를 생각해 보자. 이 두 함수는 각각 주기가 $2\pi$와 $\pi$인 주기함수이고, 두 함수의 합인 $\sin(x) + \sin(2x)$ 또한 (주기가 $2\pi$인) 주기함수이다. 아래 그래프를 참고 하도록 하자.
$ $
$ $
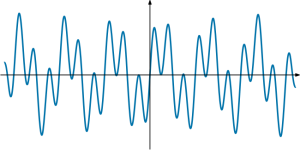
하지만 두 주기함수의 합이 언제나 주기함수가 되는 것은 아니다. 예를 들어 두 함수 $\sin(x)$와 $\sin(\pi x)$는 각각 주기가 $2\pi$와 $2$인 주기함수이지만, 두 함수의 합인 $\sin(x) + \sin(\pi x)$는 주기함수가 아니다. 아래 그래프를 보면 주기성을 띄지 않음을 확인할 수 있다.
$ $
$ $
이번 글에서는 이와 같이 두 주기함수 $f$와 $g$가 주어졌을 때, 두 함수의 합 $f+g$가 주기함수가 되기 위한 필요충분 조건을 알아보고 이를 엄밀하게 증명해 보고자 한다.
$ $
먼저 주기함수를 수학적으로 정의하는 것부터 시작하도록 하자.
$ $
$ $
함수 $f : \R \to \R$가 기본주기 $P_f$를 가지는 주기함수라 하자. 그러면 이 기본주기의 상수배는 모두 함수 $f$의 주기가 됨을 간단히 확인할 수 있다. 아래 보조정리는 이 사실의 역 또한 성립함을 보여준다.
$ $
$ $
증명. 결론에 반하여 $P = n P_f$을 만족하는 정수 $n \in \Z$가 존재하지 않는다고 가정해 보자. 그러면 나눗셈 정리에 의해 $P = m P_f + P_0$와 같이 나타낼 수 있고, 이 때의 나머지 $P_0 \in \R$은 $0 < P_0 < P_f$를 만족한다. 한 편, $P$와 $P_f$는 모두 $f$의 주기이므로 \[ f(x + P_0) = f(x + P - m P_f) = f(x) \] 가 되어 $P_0$는 $f$의 주기가 된다. 하지만 $0 < P_0 < P_f$라는 사실로부터 $P_f$가 $f$의 기본주기라는 사실에 모순이 발생한다.$ $
$ $
그렇다면 모든 주기함수는 기본주기를 가질까? 가장 단순한 반례로 상수함수를 생각해 보면 (모든 실수가 상수함수의 주기이므로) 기본주기가 존재하지 않음을 알 수 있다. 한 편, 다음과 같이 정의된 디리클레 함수(Dirichlet function) \[ D(x) = \begin{cases} 1, & \text{if} \;\; x \in \Q \\[5px] 0, & \text{if} \;\; x \notin \Q \end{cases} \] 를 생각해 보자. 이 경우, 임의의 유리수가 모두 함수 $D$가 주기가 되어 마찬가지로 기본주기가 존재하지 않음을 확인할 수 있다. 여기서 디리클레 함수는 (모든 점에서) 불연속인 함수임을 확인하자. 그렇다면 상수함수가 아니면서 연속인 주기함수는 언제나 기본주기를 가질까?
$ $
$ $
증명. 다음과 같이 함수 $f$의 주기들의 집합 $S$를 정의하자. \[ S = \set{P > 0}{f(x + P) - f(x) \; \forall \; x \in \R}. \] 이제 $P_f = \inf S \geq 0$로 정의하자. 그러면 $P_n \in S$이고 $P_n \to P_f$를 만족하는 수열 $(P_n)_{n \in \N}$이 존재한다. 그러면 $f$가 연속이라는 사실로부터 \[ f(x + P_f) = \lim_{n \to \infty} f(x + P_n) = \lim_{n \to \infty} f(x) = f(x) \] 가 되어 $P_f$는 $f$의 주기임을 알 수 있다.
$ $
이제 $P_f = 0$인 경우 $f$는 상수함수가 되어 모순이 발생함을 보일 것이다. 이를 위해 임의의 두 실수 $x,\, y \in \R$를 택하자. 그러면 (함수 $f$는 $y$에서 연속이므로) 주어진 임의의 $\varepsilon > 0$과 $z \in \R$에 대하여, 적당한 $\delta > 0$가 존재하여 \[ \abs{y-z} < \delta \; \implies \; \abs{f(y) - f(z)} < \varepsilon \tag*{$\myblue{(1)}$} \] 이 성립한다. 한 편, $P_f = 0$을 가정했으므로, $0 < P_{n_0} < \delta$를 만족하는 $P_{n_0} \in S$를 택할 수 있다. 또한 나눗셈 정리에 의해 $y - x = m P_{n_0} + r$, $0 \leq r < P_{n_0} < \delta$와 같이 나타낼 수 있다. 이제 $z := x + m P_{n_0}$을 식 $\myblue{(1)}$에 대입하고 정리하면 \[ \begin{align*} \abs{y - (x + m P_{n_0})} = \abs{r} < \delta & \; \implies \; \abs{f(y) - f(x + m P_{n_0})} < \varepsilon \\[5px] & \; \implies \; \abs{f(y) - f(x)} < \varepsilon \\[5px] \end{align*} \] 를 얻는다. 따라서 $f(x) = f(y)$이고 $f$는 상수함수라는 결론을 얻게 되어 주어진 가정과 모순이 발생한다. 따라서 $P_f > 0$이고 이로부터 $P_f$가 $f$의 기본주기임을 알 수 있다.$ $
$ $
$ $
증명. 우선 $\frac{P_f}{P_g}$가 유리수가 가정하자. 그러면 서로소인 두 양의 정수 $m,\, n$이 존재하여, $\frac{P_f}{P_g} = \frac{m}{n}$로 나타낼 수 있다. 이제 $P = n P_f = m P_g$로 정의하자. 그러면 임의의 실수 $x \in \R$에 대하여, \[ \begin{align*} f(x + P) + g(x + P) &= f(x + n P_f) + g(x + m P_g) \\[5px] &= f(x) + g(x) \end{align*} \] 가 성립한다. 따라서 $f+g$는 $P$를 주기로 갖는 주기함수이다.
$ $
역으로 $f+g$가 주기함수라 가정하자. 만약 $f+g$가 상수함수라면, 즉 임의의 실수 $x \in \R$에 대하여 $f(x) + g(x) = C$가 성립한다면, $f(x) = C - g(x)$가 되고 따라서 $P_f = P_g$임을 알 수 있다. 따라서 이 경우, 자명하게 $\frac{P_f}{P_g}$는 유리수이다.
$ $
이제 $f+g$가 상수함수가 아니라고 가정해 보자. 그러면 보조정리 2에 의해 $f+g$는 기본주기 $P_{f+g} > 0$을 갖는다. 따라서 임의의 실수 $x \in \R$에 대하여 \[ f(x + P_{f+g}) + g(x + P_{f+g}) = f(x) + g(x) \] 가 성립함을 확인할 수 있다. 이제 모순을 이끌어 내기 위하여 $\frac{P_f}{P_g}$는 유리수가 아니라고 가정해 보자. 다음으로 함수 $\gamma : \R \to \R$를 아래와 같이 정의하자. \[ \gamma(x) = f(x + P_{f+g}) - f(x) = g(x) - g(x + P_{f+g}) \] 그러면 임의의 정수 $m,\, n \in \Z$에 대하여 \[ \begin{align*} \gamma(x + n P_f + m P_g) &= f(x + n P_f + m P_g + P_{f+g}) - f(x + n P_f + m P_g) \\[5px] &= f(x + m P_g + P_{f+g}) - f(x + m P_g) \\[5px] &= \gamma(x + m P_g) \\[5px] &= g(x + m P_g) - f(x + m P_g + P_{f+g}) \\[5px] &= g(x) - f(x + P_{f+g}) \\[5px] &= \gamma(x) \end{align*} \] 를 얻는다. $\frac{P_f}{P_g}$가 무리수임을 가정했으므로, 집합 $\set{n P_f + m P_g}{m,\, n \in \Z}$는 실수 전체에서 조밀(dense)하다. 따라서 보조정리 2에 의해 $\gamma$는 상수함수여야만 한다. 따라서 적당한 실수 $C \in \R$가 존재하여, 임의의 실수 $x \in \R$에 대하여 $\gamma(x) = C$가 성립한다.
$ $
그러면 함수 $\gamma$의 정의에 의해 $f(x + P_{f+g}) = f(x) + C$이다. 그러면 \[ f(x + 2 P_{f+g}) = f((x + P_{f+g}) + P_{f+g}) = f(x + P_{f+g}) + C = f(x) + 2C \] 를 얻는다. 이와 같은 방법을 귀납적으로 계속 적용하면 임의의 양의 정수 $k \in \N$에 대하여 \[ f(x + k P_{f+g}) = f(x) + k C \] 가 성립함을 알 수 있다. 하지만 $f$는 연속인 주기함수이므로 유계(bounded)이고 따라서 $C = 0$이어야만 한다. 즉, $f(x + P_{f+g}) = f(x)$가 되므로 $P_{f+g}$는 $f$의 주기가 된다는 결론을 얻을 수 있다. 한 편, 같은 논의를 함수 $g$에도 그대로 적용하여 $P_{f+g}$는 $g$의 주기 또한 됨을 보일 수 있다. 따라서 보조정리 1에 의해 $P_{f+g}$는 $P_f$의 상수배이면서 동시에 $P_g$의 상수배이어야만 한다. 하지만 $\frac{P_f}{P_g}$가 무리수임을 가정했으므로 \[ P_{f+g} \in \set{n P_f}{n \in \N} \cap \set{m P_g}{m \in \N} = \emptyset \] 이 되어 모순을 얻는다. 따라서 $\frac{P_f}{P_g}$는 유리수가 되어야만 하고 원하는 결론을 얻는다.$ $
$ $