$ $
풀이. 점 $A$에서 선분 $BD$에 내린 수선의 발을 $P$, 점 $C$에서 선분 $BD$에 내린 수선의 발을 $R$이라고 하자.
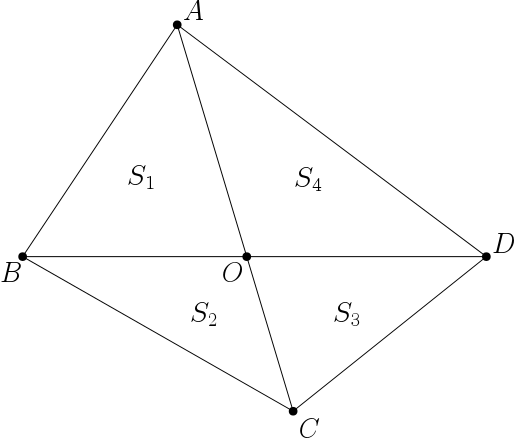
그러면 각 삼각형들의 넓이는 아래와 같이 나타낼 수 있다.
\[ S_1 = \frac{1}{2}\,\overline{BO}\,\overline{AP}, \quad S_2 = \frac{1}{2}\,\overline{BO}\,\overline{CR}, \quad S_3 = \frac{1}{2}\,\overline{DO}\,\overline{CR}, \quad \frac{1}{2}\,\overline{DO}\,\overline{AP} \]
위 식으로부터 $S_1S_3 = S_2S_4$를 얻는다. 이제 만약 $S_1$, $S_2$, $S_3$, $S_4$를 적당한 순서로 배열하여 연속적인 정수가 될 수 있다면, 적당한 정수 $n$에 대하여 이 배열을 $n, n+1, n+2, n+3$이라 할 수 있을 것이다. 이제 등식 $S_1S_3 = S_2S_4$를 만족하기 위해서는 반드시 이 배열이
\[ n(n+3) = (n+1)(n+2) \]
를 만족해야만 함을 알 수 있다. (이 외의 다른 곱셈의 조합으로는 절대 등식을 만들 수 없다.) 하지만 이 경우 $0=2$가 되어 모순이 생긴다. 따라서 $S_1$, $S_2$, $S_3$, $S_4$을 어떻게 재배열 하더라도 연속적인 정수가 될 수 없다..