$ $
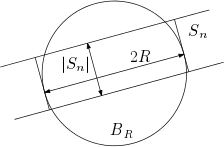
풀이. $\sum_{n=1}^{\infty} \abs{S_n} = M$이라 하자. 이제 원점이 중심이고 반지름이 $R$인 원을 $B_R$이라 하자. 그러면 임의의 $S_n$에 대하여 $B_R \cap S_n$의 넓이는 언제나 $2R\abs{S_n}$보다 작아야 한다.
$ $

$ $
따라서 아래의 부등식이 성립한다.
\[ \operatorname{area}\left( B_n \cap \bigcup_{n=1}^{\infty} S_n \right) \leq \sum_{n=1}^{\infty} \operatorname{area}(B_R \cap S_n) \leq \sum_{n=1}^{\infty} 2R\abs{S_n} = 2RM. \]
이제 반지름 $R$을 충분히 크게 잡아 $R>2M/\pi$가 되도록 하자. 그러면
\[ \pi R^2 > 2RM \geq \operatorname{area}\left( B_n \cap \bigcup_{n=1}^{\infty} S_n \right) \]
을 얻는다. 다시 말해 원 $B_R$의 넓이가 $B_R$과 $\bigcup_{n=1}^{\infty} S_n$의 교집합의 넓이보다 커지게 된다. 즉, $B_R$안에 $\bigcup_{n=1}^{\infty} S_n$에 속하지 않는 점이 반드시 존재하고 따라서 증명이 완료된다..