1. 카탈란 수의 정의 및 응용
$n$번째 카탈란 수(Catalan number) $C_n$이란 아래의 점화식을 만족하는 수열의 $n$번째 항을 말한다.
\[ C_0 = 1, \quad C_n = \sum_{i=0}^{n} C_i C_{n-i}, \ n \geq 0. \tag{1.1} \]
이 수열의 첫 10개의 항을 나열하면 다음과 같다. ($C_0$부터 $C_9$까지)
\[ 1,\ 1,\ 2,\ 5,\ 14,\ 43,\ 132,\ 429,\ 1430,\ 4862,\ \ldots \]
카탈란 수는 조합론(combinatorics)에서 빈번하게 등장하는 수 중의 하나로, 아래와 같은 문제들의 해답이 모두 $n$번째 카탈란 수 $C_n$으로 주어진다. 먼저 $C_4 = 14$라는 사실을 기억하자. (더 많은 예제들은 Wikipedia에서 찾아 볼 수 있다.)
- $C_n$은 $n$ 쌍의 여는 괄호(open parenthesis '$($') 와 닫는 괄호(closed parenthesis '$)$')로 만들 수 있는 올바른 괄호 구조의 가짓수와 같다. 예를들어 $4$쌍의 열린 괄호와 닫는 괄호로는 아래의 $14$가지 경우의 수가 나온다.
\[ \begin{aligned}
& (((()))),\ (())(()),\ (()()()),\ ()((())),\ ()(()()),\ ()()(()),\ (()(())), \\[5pt]
& ()()()(),\ ((()())),\ ()(())(),\ ((()))(),\ (()())(),\ (())()(),\ ((())()).
\end{aligned} \]
- $C_n$은 $n+1$개의 항에 이항연산을 적용하는 순서의 가짓수와 같다. 예를 들어 $5$개의 문자 $a,\, b,\, c,\, d,\, e$에 괄호로 이항연산의 순서를 표현하면 아래의 $14$가지 경우가 나온다.
\[ \begin{aligned}
& (((ab)c)d)e,\ ((ab)(cd))e,\ (ab)((cd)e),\ ((ab)c)(de), \\[5pt] & a(b(c(de))),\ a((bc)(de)),\ (a(bc))(de),\ (ab)(c(de)), \\[5pt] & ((a(bc))d)e,\ (a((bc)d))e,\ a(((bc)d)e), \\[5pt] & a(b((cd)e)),\ a((b(cd))e),\ (a(b(cd)))e.
\end{aligned} \]
- $C_n$은 $n+2$각형을 $n$개의 삼각형으로 나누는 방법의 개수이다. 아래 그림은 $6$각형을 $4$개의 삼각형으로 나누는 $14$가지 경우를 모두 나타낸 것이다.
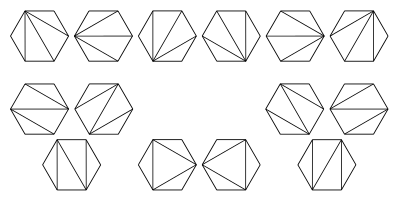
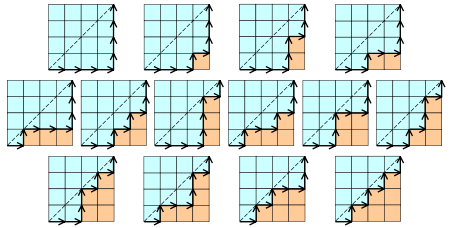
- $C_n$은 $n \times n$ 격자의 왼쪽 아래 꼭지점 $(0,\,0)$에서 오른쪽 위 꼭지점 $(n,\,n)$을 향해 최단거리로 이동하는 경우의 수 중 직선 $y=x$을 넘어가지 않는 경우의 수와 같다. $4 \times 4$ 격자에서 가능한 $14$가지 경우가 아래쪽 그림으로 주어져 있다.
- $C_n$은 높이가 $n$인 계단 모양을 $n$개의 직사각형으로 완전히 채울 수 있는 경우의 수와 같다. 예를들어, 높이 $4$인 계단 모양을 $n$개의 직사각형으로 채우면 다음의 $14$가지 경우가 나온다.

$ $
2. 카탈란 수의 계산
이번에는 생성함수를 이용하여, 카탈란 수열이 아래의 식을 만족함을 보일 것이다.
정리. 모든 $n \geq 0$에 대하여, 카탈란 수(Catalan number) $C_n$은 아래 식을 만족한다.
\[ C_n = \frac{1}{n+1}{2n \choose n} = \frac{(2n)!}{(n+1)!n!} \qquad \text{for} \quad n \geq 0. \]
증명. 먼저 $C_n$의 생성함수 $c(x)$를 아래와 같이 정의하자.
\[ c(x) = \sum_{n=0}^{\infty} C_n x^n. \tag{2.1} \]
$C_n$의 점화 관계식 $(1.1)$을 이용하여 식 $(2.1)$을 다시 정리하면,
\[ \begin{aligned}
c(x) & = C_0 + \sum_{n=1}^{\infty} C_n x^n = 1 + \sum_{n=0}^{\infty} C_{n+1} x^{n+1} \\[5pt]
& = 1 + \sum_{n=0}^{\infty} \left( \sum_{i=1}^{n} C_i C_{n-i} \right) x^{n+1} = 1 + x \sum_{n=0}^{\infty} \left( \sum_{i=1}^{n} C_i C_{n-i} \right) x^n \\[5pt]
& = 1 + x \left(\sum_{n=0}^{\infty} C_n x^n \right)^2 = 1 + x c(x)^2.
\end{aligned} \]
위 식에서 $5$번째 등식은 $\left(\sum_{n=0}^{\infty} C_n x^n \right)^2$에서 $x^n$항의 계수가 $\sum_{i=1}^{n} C_i C_{n-i}$와 같다는 사실에서 간단히 성립한다. 따라서 $x c(x)^2 - c(x) + 1 = 0$이 성립하고 이를 정리하면,
\[ c(x) = \frac{1 + \sqrt{1-4x}}{2x} \qquad \text{or} \qquad \frac{1 - \sqrt{1-4x}}{2x} \]
를 얻는다. 이제, $\lim_{n \to 0^+} c(x) = C_0 = 1$이란 사실을 이용하면,
\[ \begin{aligned}
\lim_{n \to 0^+} \frac{1 + \sqrt{1-4x}}{2x} & = \infty, \\[5pt]
\lim_{n \to 0^+} \frac{1 - \sqrt{1-4x}}{2x} & = \lim_{n \to 0^+} \frac{2}{1 + \sqrt{1-4x}} = 1.
\end{aligned} \]
그러므로 첫번째 해는 $c(x)$의 해가 될 수 없고, 결과적으로
\[ c(x) = \frac{1 - \sqrt{1-4x}}{2x} \tag{2.2} \]
를 얻는다. 이제 일반화된 이항정리 (Newton's generalized binomial theorem)를 이용하자. 우선 모든 $y$에 대하여 다음의 등식이 성립한다.
\[ \sqrt{1+y} = \sum_{n=0}^{\infty} {\frac{1}{2} \choose n} y^n. \tag{2.3} \]
이제 $n \geq 1$에 대하여, 위 식의 ${\frac{1}{2} \choose n}$ 부분을 정리하면,
\[ \begin{aligned}
{\frac{1}{2} \choose n} & = \frac{\frac{1}{2} \left(-\frac{1}{2}\right) \left( -\frac{3}{2}\right) \cdots \left( \frac{1}{2} -n + 1 \right)}{n!} \\[5pt]
& = \frac{\frac{1}{2} \left(-\frac{1}{2}\right) \left( -\frac{3}{2}\right) \cdots \left( \frac{3-2n}{2} \right)}{n!} \\[5pt]
& = \frac{(-1)^{n-1}}{2^n n} \cdot \frac{1 \cdot 3 \cdots (2n-3)}{(n-1)!} \\[5pt]
& = \frac{(-1)^{n-1}}{2^n n} \cdot \frac{1 \cdot 2 \cdot 3 \cdots (2n-3)(2n-2)}{(n-1)!} \cdot \frac{1}{2 \cdot 4 \cdots (2n-2)} \\[5pt]
& = \frac{(-1)^{n-1}}{2^n n} \cdot \frac{(2n-2)!}{(n-1)!} \cdot \frac{1}{2^{n-1}(n-1)!} \\[5pt]
& = \frac{(-1)^{n-1}}{2^{2n-1} n} \cdot \frac{(2n-2)!}{(n-1)!(n-1)!} \\[5pt]
& = -\frac{2}{n}\left(\frac{-1}{4}\right)^n {2n-2 \choose n-1} \end{aligned} \]
따라서 위의 결과와 식 $(2.3)$으로부터 아래의 결과를 얻는다.
\[ \sqrt{1+y} = \sum_{n=0}^{\infty} {\frac{1}{2} \choose n} y^n = 1 + \sum_{n=1}^{\infty} {\frac{1}{2} \choose n} y^n = 1 - 2 \sum_{n=1}^{\infty} {2n-2 \choose n-1} \left(\frac{-1}{4}\right)^n \frac{y^n}{n}. \]
이제 위 식에 $y = -4x$를 대입하고 정리하면,
\[ \begin{aligned}
c(x) & = \frac{1 - \sqrt{1-4x}}{2x} \\[5pt]
& = \frac{1}{2x} - \frac{1}{2x} \left( 1 - 2 \sum_{n=1}^{\infty} {2n-2 \choose n-1} \left(\frac{-1}{4}\right)^n \frac{(-4x)^n}{n} \right) \\[5pt]
& = \frac{1}{2x} - \frac{1}{2x} \left( 1 - 2 \sum_{n=1}^{\infty} {2n-2 \choose n-1} \frac{x^n}{n} \right) \\[5pt]
& = \sum_{n=1}^{\infty} {2n-2 \choose n-1} \frac{x^{n-1}}{n} \\[5pt]
& = \sum_{n=0}^{\infty} {2n \choose n} \frac{x^n}{n+1}.
\end{aligned} \]
따라서
\[ c(x) = \sum_{n=0}^{\infty} {2n \choose n} \frac{x^n}{n+1} \tag{2.4} \]
를 얻고, 마지막으로 식 $(2.1)$와 $(2.4)$의 계수를 비교하면 원하는 결과를 얻는다.


